Supposing I were to tell you that I know three people: an average-sized kid, a regular-sized adult, and a beanpole of a basketball player. Let’s assume that, earlier today, I used my handy-dandy tape measure to determine that the kid is exactly 4-feet tall, the adult is 6-feet tall, and the basketball player is 8-feet tall.
Now, suppose I were to inform you that these three people are currently in close proximity to each other and they are all looking in the same direction. Assuming that there’s nothing to block anyone’s view, which of these characters do you think will be able to see the farthest?
Your initial reaction may be to choose the basketball player, but you are making a number of assumptions, not the least being that you are assuming all these characters are standing up. It might be that the adult is ensconced in a comfy chair while the basketball player is kneeling down, for example (you have to be careful discussing things with engineers because we can be tricky little scallywags if we want to be).
Even assuming that all three of our subjects are standing up, we still can’t guarantee that the basketball player has the advantage. This is because we haven't specified their relationship to each other, which could be as illustrated below.
 It's hard to compare things if you don’t first set the ground rules (Image source: Max Maxfield)
It's hard to compare things if you don’t first set the ground rules (Image source: Max Maxfield) The thing is that it can be hard to compare things if we don’t first set the ground rules (no pun intended). In this case, for example, on the left, we find our 6-foot adult standing on the ground, which places his head six feet above ground level. In the middle, our 4-foot tall kid is standing on a 4-foot tall box, which results in his head being eight feet above the ground. Meanwhile, on the right, our unfortunate 8-foot tall basketball player finds himself standing in a 4-foot deep hole (I hate it when that happens), which leaves his head only four feet above the ground. The end result is that, in this scenario, it’s the 4-foot kid who can see the farthest.
 It’s important to establish a common frame of reference (Image source: Max Maxfield)
It’s important to establish a common frame of reference (Image source: Max Maxfield) The point of all this is that it’s possible for us to measure people’s heights individually, but -- depending on what we are trying to do -- it may be meaningless to compare them with each other unless we first establish some common frame of reference. In the case of our three test subjects, for example, our original question -- “Which one will be able to see the furthest?” -- makes much more sense if we also specify that they are all to be standing close to each other on a level piece of ground as illustrated above, in which case the basketball player will, not surprisingly, have the advantage.
Miscellaneous Meters
In earlier columns, we’ve introduced the concepts of voltage (measured in volts), current (measured in amps), and resistance (measured in ohms).
It may not surprise you to learn we have tools we can employ to measure these little rascals: we can use voltmeters to measure voltage, ammeters to measure current, and ohmmeters to measure resistance. We also have multimeters, which can measure voltage, current, and resistance, along with a variety of other things, depending on the meter.
In the early days (circa the late 1800s and early 1900s), all of these meters were analog in nature, using a moving pointer to display the reading. Later, digital meters with numeric displays arrived on the scene. Today, it’s possibly to purchase analog and digital versions of all these meters.
In a future column, we will talk about digital multimeters in more detail, including where to get them and how to use them to measure things. For the purposes of this column, however, let’s simply assume we have a digital voltmeter, which we can use to measure the voltage difference (more formally, the electric potential difference) between two points in an electric circuit.
A Rose by Any Other Name
The phrase "A rose by any other name would smell as sweet" is a popular reference to William Shakespeare's play Romeo and Juliet. (This formulation is actually a paraphrase of the Bard’s original words, which were: “What's in a name? That which we call a rose by any other name would smell as sweet.”)
The “rose by any other name” reference is often used to imply that the names of things do not affect what they really are. The reason I’m waffling on about this here is that it’s strangely apt with regard to the labels we assign to voltages. Consider a 5-volt battery for example. Suppose we were to use our digital voltmeter to measure the electrical potential between its terminals. We might illustrate this as shown in (a) below.
 Using a digital voltmeter to measure a 5-volt battery (Image source: Max Maxfield)
Using a digital voltmeter to measure a 5-volt battery (Image source: Max Maxfield) Observe that the meter has a black terminal/wire/probe and a red terminal/wire/probe. The black terminal on the meter is usually annotated COM (for “common”). The black probe is typically applied to the more negative of the pair of points we are measuring, while the red probe is typically applied to the more positive of the pair. In the case of our example (a), this will result in the display showing 5.000, thereby indicating +5 V.
What would happen if we were to apply the probes the other way round? Observe that I didn’t say “the wrong way round” because “wrong” doesn’t have any meaning in this context. In this case, all that would happen is that the display would show -5.000, thereby indicating -5 V as shown in (b) above.
All this leads to an obvious question (well, obvious once we’ve thought to ask it), which is “Why did we use the labels 0 V and 5 V in the above diagram. After all, in Part 4 we explained how our battery is actually formed from two compartments, one filled with positive (+ve) ions and the other filled with negative (-ve) ions. On this basis, wouldn’t it be technically more correct and/or make more sense to use the labels +2.5 V and -2.5 V as illustrated below?
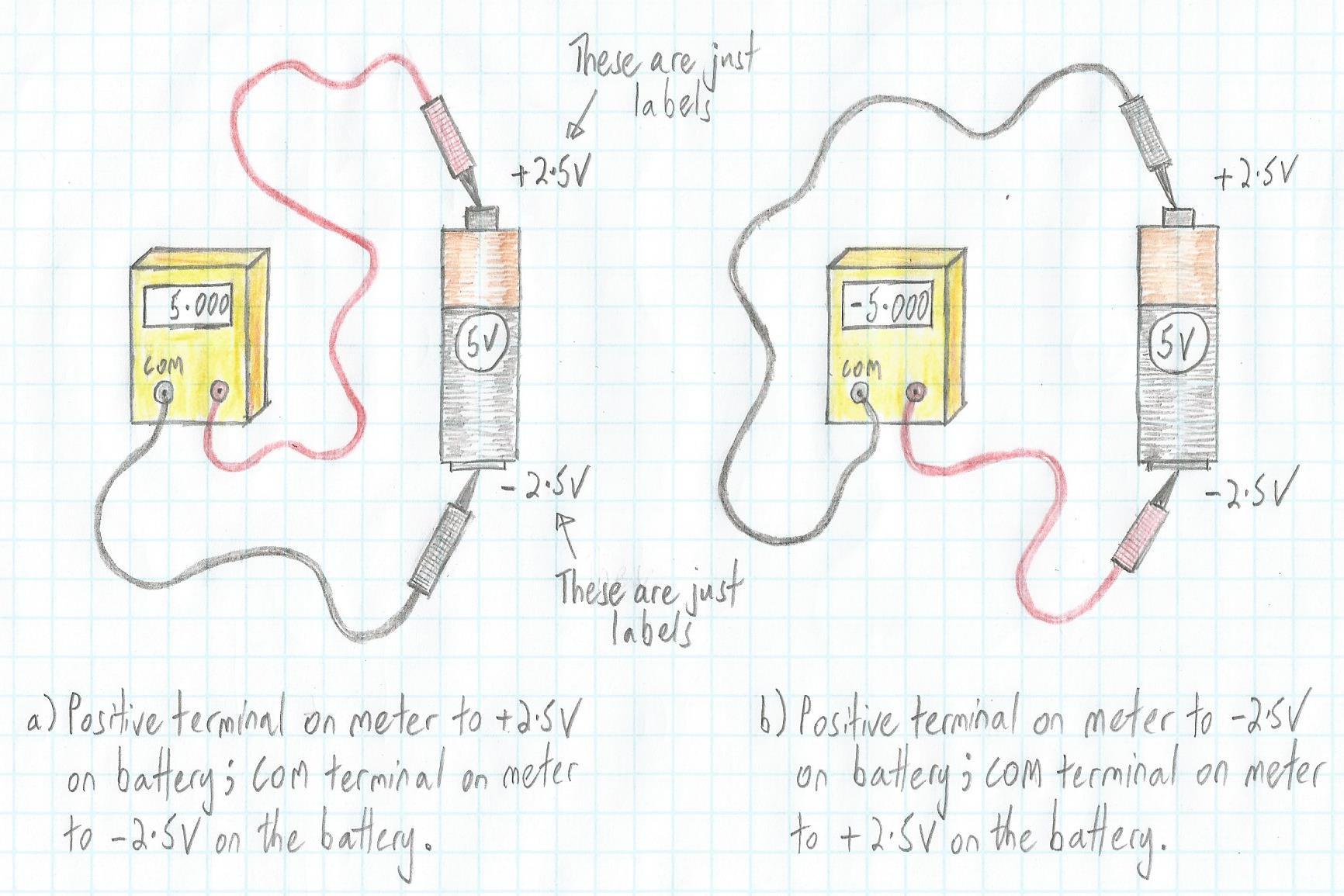 Associating labels of +2.5 V and -2.5 V with our 5-volt battery (Image source: Max Maxfield)
Associating labels of +2.5 V and -2.5 V with our 5-volt battery (Image source: Max Maxfield) Well, irrespective as to whether using +2.5 V and -2.5 V seems to make more sense, the fact of the matter is that 5 V, 0 V, +2.5V, and -2.5V are just labels we are writing on a piece of paper. Observe that the voltmeter reads the same as before because it’s measuring the real, physical voltage differential between the two points. In reality, it doesn’t matter what labels we employ, although it’s certainly true to say that some will be less useful than others; for example, “Cheddar” and “Noodle” spring to mind as being... let’s say “unhelpful.”
We will return to this point shortly. For the moment, let’s stick with our 0 V and 5V labels. Now suppose that we have two unrelated 5-volt batteries and we apply our voltmeter as illustrated below.
 First experiment with two unrelated 5-volt batteries (Image source: Max Maxfield)
First experiment with two unrelated 5-volt batteries (Image source: Max Maxfield) In this case, the voltmeter will show 0.000 because -- much like our example earlier with the kid standing on a box, the adult standing on the ground, and the basketball player standing in a hole -- there is no common point of reference between the two batteries.
Let’s take this one step further. Suppose we use each of our batteries to implement voltage dividers and we measure various voltages as illustrated below.
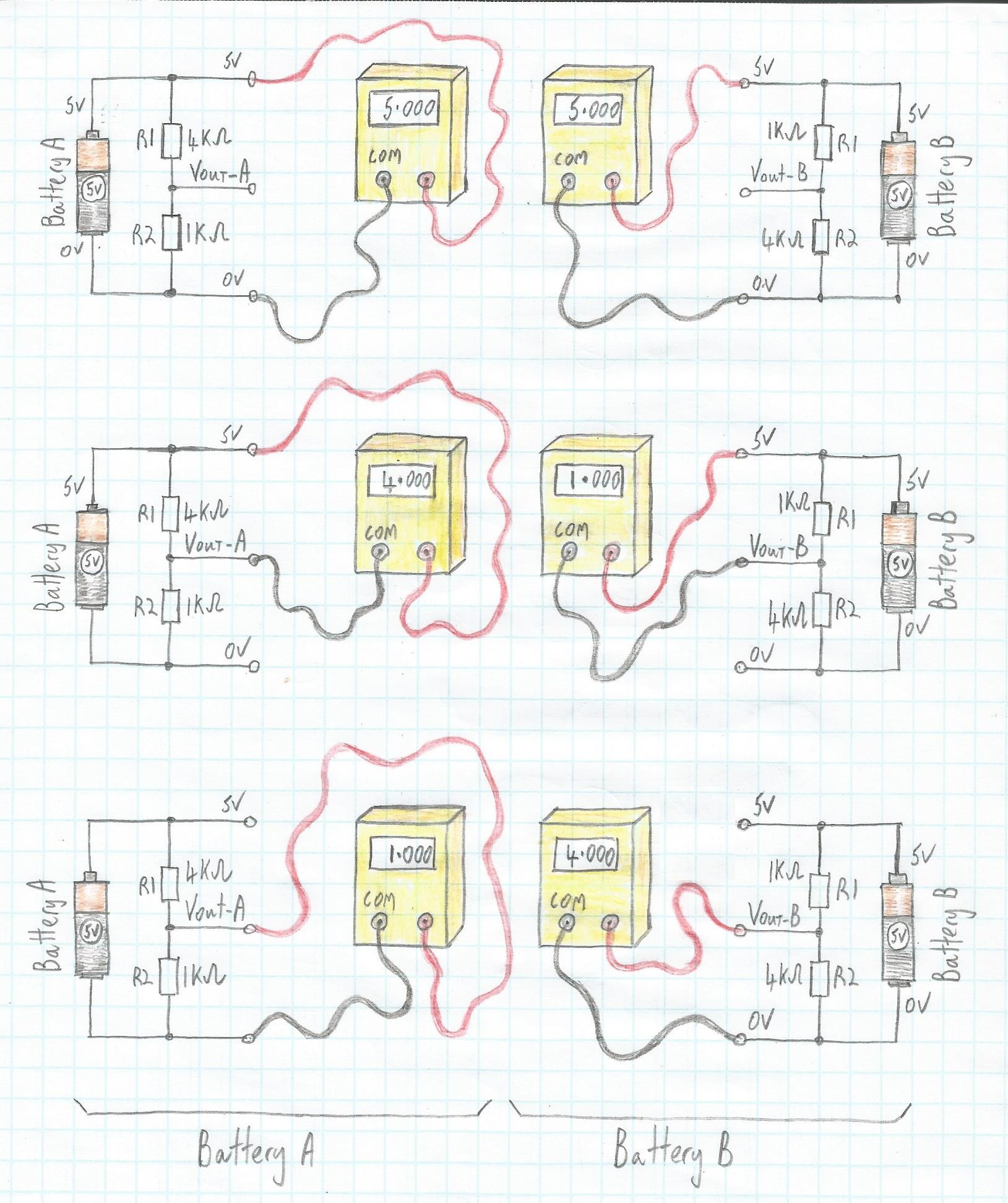 More experiments with two unrelated 5-volt batteries (Image source: Max Maxfield)
More experiments with two unrelated 5-volt batteries (Image source: Max Maxfield) Remember that we introduced voltage dividers in Part 7, including the equations we can use to determine the various voltage drops across the resistors forming the divider.
So, what do you think will happen if we attempt to measure the voltage difference between signals Vout-A and Vout-B? Well, once again, as illustrated in (a) below, the voltmeter will show 0.000 because we don’t have a common point of reference.
 Adding a common point of reference (Image source: Max Maxfield)
Adding a common point of reference (Image source: Max Maxfield) By comparison, if we connect the 0 V sides of both batteries to provide a common point of reference -- which would be the counterpart of our example with the kid, adult, basketball player all standing on a level piece of ground -- it now becomes meaningful to measure the voltage difference between Vout-A and Vout-B as illustrated in (b) above.
Let’s take this one step further. Suppose we keep battery A as 5 V, but we swap out our 5 V battery B for a 10 V battery C as illustrated below.
 Working with multiple disparate voltage sources (Image source: Max Maxfield)
Working with multiple disparate voltage sources (Image source: Max Maxfield) I think this last example makes it abundantly clear why we typically like to think of our common point of reference -- the one from which all other voltages in the circuit are measured -- as being 0 V, because it helps us make sense of all our subsequent readings.
Feeling Grounded
It’s common to hear engineers refer to the common point of reference as "ground" (often written as GND) and "earth." The reason this came about is that, for measurement purposes, the Earth itself can serve as a (reasonably) constant potential reference against which other potentials can be measured. Furthermore, the ground or earth in a mains (AC powered) electrical wiring system is a conductor that provides a low-impedance path to the Earth to prevent hazardous voltages from appearing on equipment. Thus, in many cases -- like the electric power supplied to your home -- this reference point is literally a metal spike driven into the earth or ground.
 A typical earthing electrode (left of gray pipe), consisting of a conductive rod driven into the ground, at a home in Australia (Image source: Wikipedia/Ali K)
A typical earthing electrode (left of gray pipe), consisting of a conductive rod driven into the ground, at a home in Australia (Image source: Wikipedia/Ali K) Electrical and electronic circuit diagrams often make use of special ground symbols. In fact, there are a variety of such symbols that can be used to represent different things, such as chassis ground, analog (a.k.a. circuit ground), digital (a.k.a. signal ground), reference ground, and so forth.
Generally speaking, the symbol beginners see the most is the standard earth/ground symbol -- three decreasing horizontal bars -- as illustrated below.
 The standard earth/ground symbol (Image source: Max Maxfield)
The standard earth/ground symbol (Image source: Max Maxfield) For many purposes, including the discussions in these columns, the earth ground signal is used as a common ground signal and a 0 V reference.
Last, but not least (at least, for this column), earlier we used the phrase “Electrical and electronic circuit diagrams...” Did you say to yourself, “I wonder what’s the difference?” Well, if the truth be told, the distinction between electrical and electronic systems can be a bit fuzzy.
One way to think about this is that electric/electrical systems use electricity to transmit and manipulate power, while electronic systems use electricity to transmit and manipulate information.
Another point of view is that electrical systems consist only of energy sources, wires, and so-called passive components like resistors, capacitors, and inductors, while electronic circuits also feature active components like diodes, transistors, and integrated circuits (popularly known as "silicon chips") that are formed from esoteric materials known as semiconductors (we'll be discussing these concepts in more detail later in this series).
OK, that’s it for this column. I can’t wait for you to see what’s coming next. In the meantime, as always, I appreciate your comments, questions, and suggestions.
 max
max
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.
[this comment has been deleted]
You are a waste of space -- please stop posting dross comments like this
Are you sure? yes | no
Another good one but this time I might have some odd dreams involving meter leads tonight :-)
Are you sure? yes | no
Welcome to my world LOL
Are you sure? yes | no