
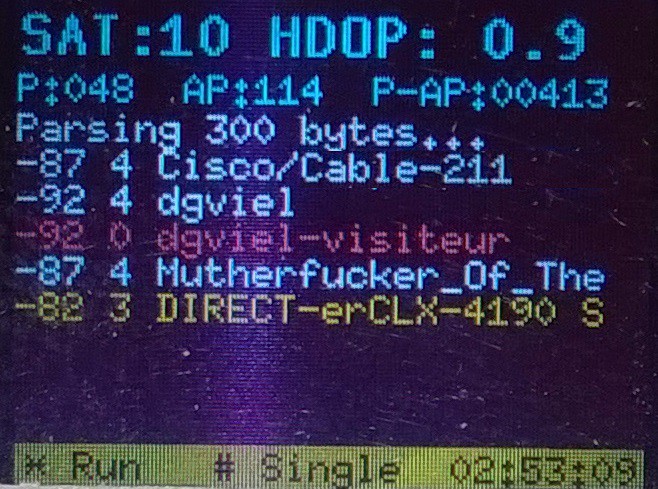
Back home the data is dumped on my PC,
imported in a MS Access database (to simplify some math) and a HTML file
calling Google Maps is generated.
The router name in red is open. The yellow
one is WEP or WPA_PSK or WPA2_PSK. The white ones are WPA_WPA2_PSK.
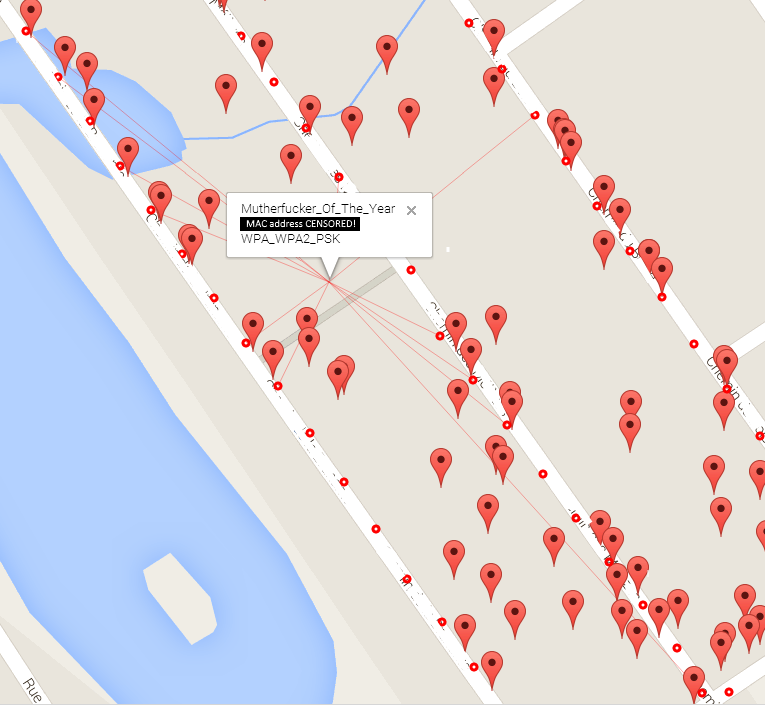
The red dots are the sampling points. The markers are the other routers. The red lines show the points that were used to triangulate. The streets names and the MAC address were erased on purpose.
Disclaimer: This is an approximate triangulation and the signal strength depends where is the source inside the home which impact the results. Also, the triangulation I’m doing is kinda wrong. You cannot just use the coordinates as XY like I did because they are on a sphere but for short distance it's OK.
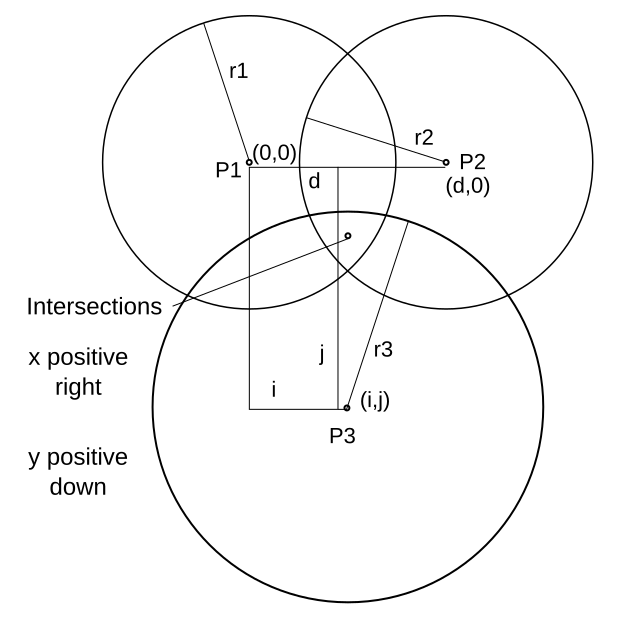
Triangulation
To understand how I did it, see the triangulation as vectors with different signal strengths. Each one "pulling" with its own strength. All of the triangulation computing is done with some queries in the database. This saves A LOT of code.
The RSSI (Received signal strength indication) is an attenuation given in negative dB: -90db is less than -60dB and so on. To simplify things, I work with positive numbers as a kind of “signal strength”:
Strength = (100 + RSSI)Why 100? Because the RSSI given by the ESP never goes below -99dB. So a -90dB signal give me a strength of 10, -60dB = 40 and so on.
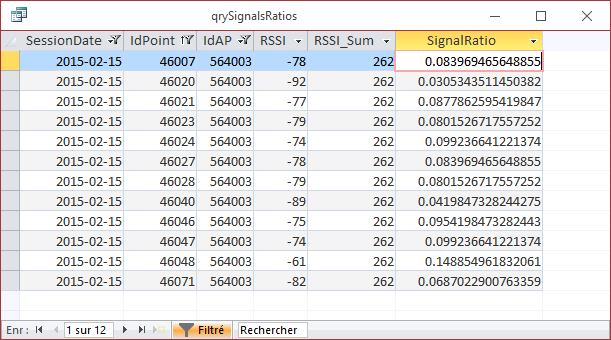
Some simple math now. For a given Access Point (AP) I do a sum of all the measured signal strength: let's call it [RSSI_Sum].
Then for each sample (Strength @ coordinate) I compute a strength ratio (the vector "Strength"):
SignalRatio_@LatLong1 = Strength_@LatLong1 / [RSSI_Sum]
SignalRatio_@LatLong2 = Strength_@LatLong2 / [RSSI_Sum]
...
SignalRatio_@LatLong_n = Strengt_@LatLong_n / [RSSI_Sum]Here is some partial results:
Then I triangulate (ok, approximate a triangulation) the lat/long by doing a sum of... I don't know how to explain it in English...
For each GPS coordinate I do apply the SignalRatio of that coordinate then sum them all:
Latitude = Sum( Lat_n * [SignalRatio_n] )
Longitude = Sum( Long_n * [SignalRatio_n] )Kind look like this in SQL:
SELECT SSID, Sum(Lat*[SignalRatio]) AS Lat, Sum(Lng*[SignalRatio]) AS Lng
FROM …
GROUP BY SSID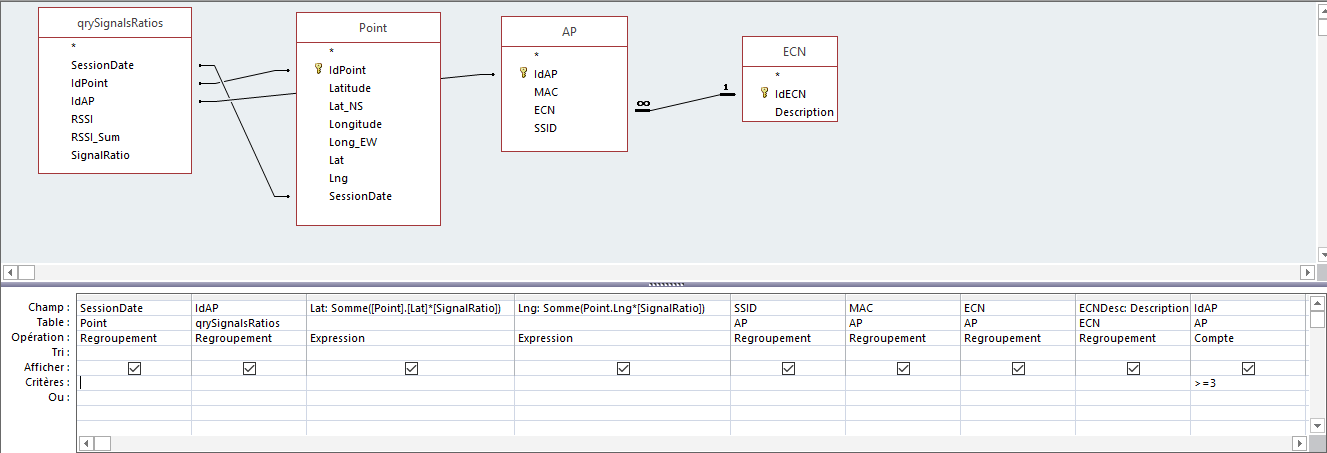
It's a really rough triangulation because the coordinates are on a sphere (our planet) but I think it's OK for a few meters.
Finally, a dotNET app is used to build a HTML file with some generated JavaScript for the Google Maps API. It’s ugly but for a one-time project that’s OK.
There you are MutherF***er…







 Jesse R
Jesse R
 bafeigum
bafeigum
 Phil Handley
Phil Handley
 Igor Brkic
Igor Brkic
Would you be able to share more information on this project (source code, schematic, etc). There is someone in my sisters neighborhood who has named their Access Point... something very disturbing (doing perverted, unspeakable acts to children), and I want to have a little discussion with this individual.
I planned on writing some code to accomplish the same trilateration concept that you have done, and thought I would reach out to you to see if you would be willing to share some more specific on your project in order to save me time.
Thanks.