Introduction
Proof of concept - running deep neural network with 170 neurons on Atmega328 - Arduino.
I used MNIST dataset - handwritten digits 28x28 pixels, downsampled to 9x9

Network topology is fully connected, with ReLU activation in two hidden layers and linear activation in output layer
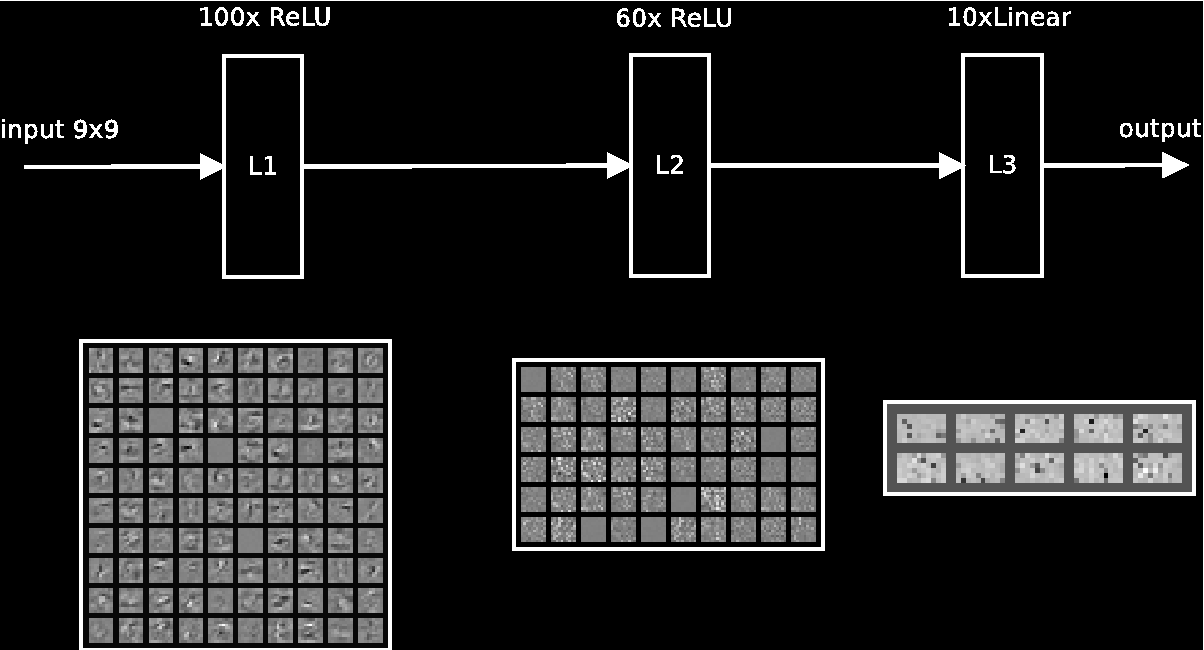
Network was trained on GPU (gtx1080) on my own neural network framework. After learning, weights have been rouded and mapped into 8 bit fixed point.
Weights mapping
It is no wise to store weights as floats on 8 bit mcu. Each weight needs 4 bytes of memory, and each float operation is more than 10-times slower than int on AVR.
We need to store
layer 1 : (9x9 + 1)*100
layer 2 : (100+ 1)*60
layer 3 : (60+ 1)*10
= 14870 synapses
Converting into 8bit char is necessary. note : extra weight +1 is for bias
I used simple linear mapping :
weights are stored in separated .h files (each for one layer) :
#define layer_1_scaling_factor 515
signed char weights_layer_1[8200]={
-34, -17, -4, 18, 24, -9, 8, -7 ... };
Importat for AVR implementation is to store weights into flash :
const signed char weights_layer_1[8200] PROGMEM={ ...
after this you can't access array like :
value = array[idx];
you need to use :
value = pgm_read_byte(&array[idx]);
Storing outputs in ram
To save some ram memory (we have only 2k) I used two buffers trick, and exchanging only pointers. The most wide layer is 101ints wide. We need two buffers of ints, 101*2*2bytes = 404 bytes to store layers outputs.

At beginning, there are two buffers (each 101 ints) initialized. When processing network, data are stored into buffer A which is input for layer 1, and its output is stored into buffer B. Buffer B is input for layer 2, and so on ...
Layer computing kernel
is nothing else than vector matrix multiplication, I used some unrolling tricks (30% speed increase on intel i5), on ARM Cortex M4 it similar, because of pipeline :
void matrix_vector_dot_kernel(t_nn_buffer *output, t_nn_buffer *input,
signed char *weights,
unsigned int input_size,
unsigned int output_size,
unsigned int weights_scaling)
{
unsigned int w_ptr = 0;
for (unsigned int j = 0; j < output_size; j++) {
unsigned int input_ptr = 0;
unsigned int size = input_size+1;
long int sum = 0;
while (size >= 4) {
sum+= (weights[w_ptr]*input[input_ptr]); w_ptr++; input_ptr++;
sum+= (weights[w_ptr]*input[input_ptr]); w_ptr++; input_ptr++;
sum+= (weights[w_ptr]*input[input_ptr]); w_ptr++; input_ptr++;
sum+= (weights[w_ptr]*input[input_ptr]); w_ptr++; input_ptr++;
size-= 4;
}
while (size) {
sum+= (weights[w_ptr]*input[input_ptr]); w_ptr++; input_ptr++;
size--;
}
sum = (sum*weights_scaling)/(127*1000);
output[j] = sum;
}
}
Results
There is no significant loss of accuracy -> I compared 32 bit float weights with 8 bit signed char :

Finally, I runned network on avr atmega328, with the same result :
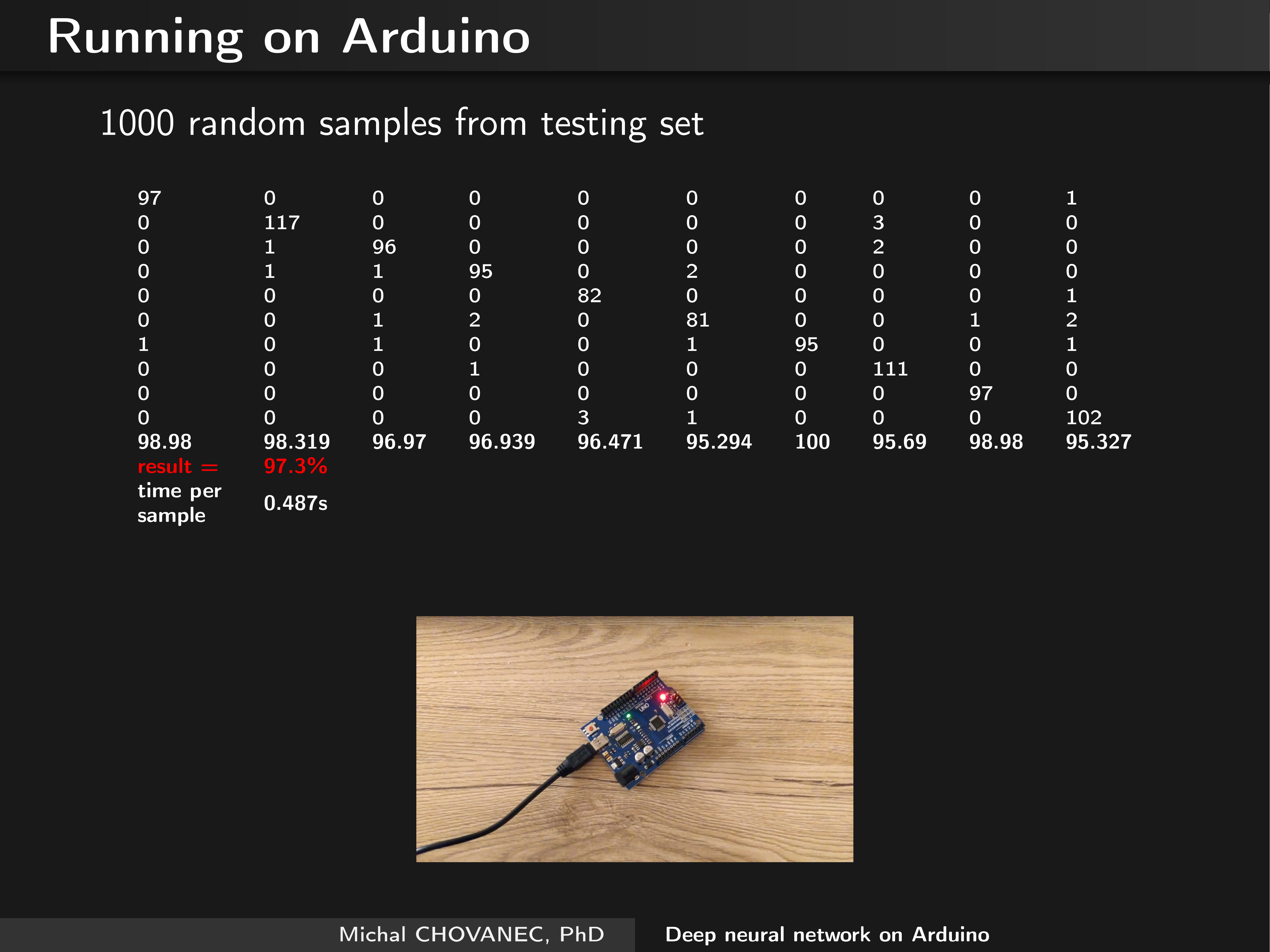
short video I made is here :
 michal.nand
michal.nand

 Sumit
Sumit
 Foxmjay
Foxmjay
 daovanhoa12
daovanhoa12
 Kuro
Kuro
Could you give me your project link? thx!