- Audio filter implementations
All of these implementation use a multiply-and-accumulate (MAC) scheme to compute each of the terms on the right side of the following equation, then divides bya(1), if necessary. Some of the implementations are serial, some are parallel. Some are fixed point, some floating.
a(1)*y(n) = b(1)*x(n) + b(2)*x(n-1) + ... + b(nb+1)*x(n-nb) - a(2)*y(n-1) - ... - a(na+1)*y(n-na)The actual filter form implemented was the Direct Form Type I transposed similar to what Matlab uses for its
If a(1) is not equal to 1, you must divide the right side by a(1).filterfunction. This means that the Matlab filter design funcitons (which yield the a's and b's) can be used to design filters. Input is from the audio codec and output is back to the audio codec.
There are a set of modules which are needed for all of the test programs below which interface to the audio codec. They are: cpuclockPLL.v, I2C_AV_Config.v, I2C_Controller.v, Reset_Delay.v, AUDIO_DAC_ADC.v and VGA_Audio_PLL.v. Each of the filter implementations has one top level module which needs to be incorporated into the project (using the menu item: project>Add/Remove files in project). The project with all top-level modules and interfaces is zipped here (QuartusII version 8.1). All of these filters receive input from the audioline-in(blue phone jack) and send output to audioline-out(green phone jack). The project archive (QuartusII version 10.1) using 18-bit fixed point filters (and a slightly different audio out register structure) is here.
General second, fourth and sixth order IIR (18-bit fixed point) .
The first implementation top-level module has modules for 2, 4, and 6th-order IIR audio filters synched to run once/audio sample (about 47 KHz). Each filter runs in parallel with all the other filters and each filter uses one 18-bit multiplier, so that you could implement up to about 35 filters. The filters use 18-bit, 2's complement notation with 16 bits of fraction for both the signal and the coefficients. This means that all filter coefficients have to be scaled to the range-1<coefficient<1. The matlab code to do the scaling and conversion to hex constants will produce estimates of the scaled constants which you must check for being in range.
A matlab program to form the Verilog to specify the filter is at the end of the Verilog file as a comment. Typical Verilog filter code generated by the Matlab program is shown below. You must rename the module, and substitute in appropriate input and output variable names. The matlab program computes the a and b values, scales them to avoid overflow, and converts them to hex. The matlab program also plots the exact filter solution as well as the scaled 16-bit approximation. Always check the approximation to verify filter quality. The book Digital Signal Processing and the microcontroller was very useful for this code (see reference below).
An example of the generation of filters by creating the filter Verilog code in Matlab. The normalized filter cutoffs (frequency/(Fs/2)) are[0.1 0.2], for a 4th order filter, and scaled by>>>2. Always check the approximation to verify filter quality. The plot below shows the result of coefficient truncation error on filter response.
//Filter: cutoff=0.100000 //Filter: cutoff=0.200000 IIR4 filter( .audio_out (your_out), .audio_in (your_in), .scale (3'd2), .b1 (18'h149), .b2 (18'h0), .b3 (18'h3FD6E), .b4 (18'h0), .b5 (18'h149), .a2 (18'hCD98), .a3 (18'h2F54E), .a4 (18'hA42E), .a5 (18'h3D6F5), .state_clk(AUD_CTRL_CLK), .lr_clk(AUD_DACLRCK), .reset(reset) ) ; //end filter
![]()
General second, fourth and sixth order IIR Filter (27-bit fixed point) .
This implementation extends the precision of the filters to allow accurate, lower bandwidth filters. As before the code modularizes the IIR filters and simplifies the generation of filters by creating the filter Verilog code in Matlab. The current...
0%
0%
DSP in Verilog: when it needs to be FAST
IIR filters, CIC filters, Direct Digital Synthesis, Karplus-Strong string synthesis, Adaptive noise cancellation, soft radio
 Bruce Land
Bruce Land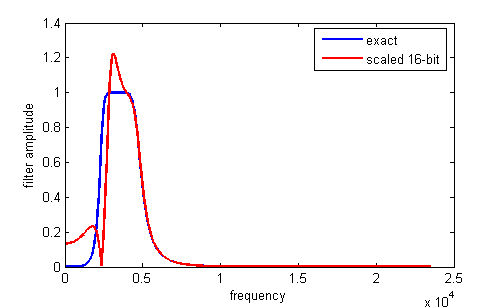

 NotBlackMagic
NotBlackMagic
 Guido
Guido
 zpekic
zpekic