The design goals of low cost have been met. I
think this is about as cheap as one can build a 3D printer. Looking
back, going straight from repstrapping to building a printer like this
has been very challenging and educational. Lots of fun and learning has
taken place. Overall it has been a great learning experience. As the
saying goes, everything is hard before it's easy. For example, when I
started this project I didn't know how to use CAD. I have definitely
learned a lot in the process.
I'll be shelving this project, it has met its goals of being super cheap and printable.
This
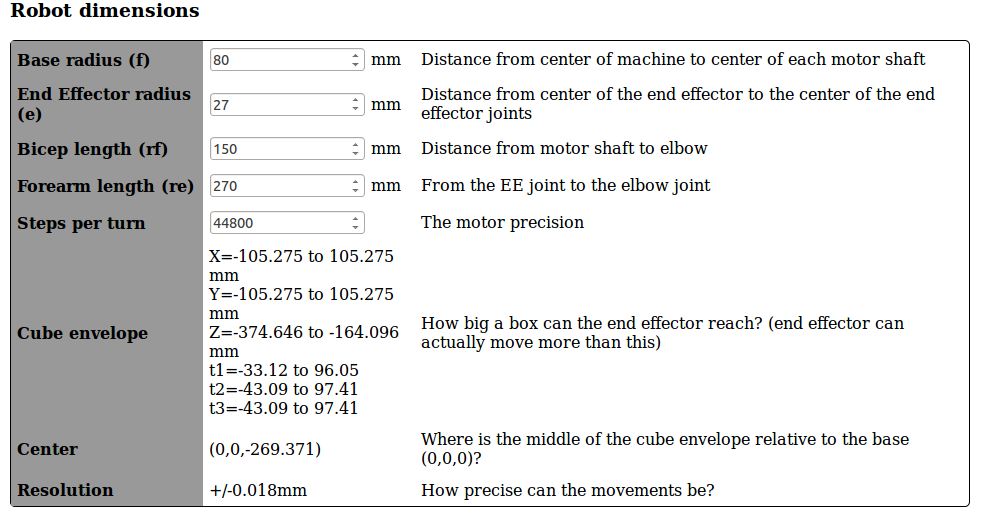
hasn't been without cost though. Calibration is very tricky. All parts
must be produced and measured precisely to be able to print anything at
all!
Dialing it in is very time consuming. Calibration is not
impossible, it must simply be done in a logical order, making sure at
every step that every part is measured accurately.
This leads me
to the next design phase. I would like to design a Reprap that is easy
to calibrate, has a rock bottom bill of materials, highly printable, and
can reprint copies of its own parts. All this while maintaining
accuracy of the parts.
I hope you enjoyed reading!
P.S. I have set up a new project page.
Credits
Special thanks goes to Matt Kimbal for teaching me how to use FreeCad. I would also like to thank the Firepick Delta team for inspiring this project. Without you guys this project would not have been.
 TTN
TTN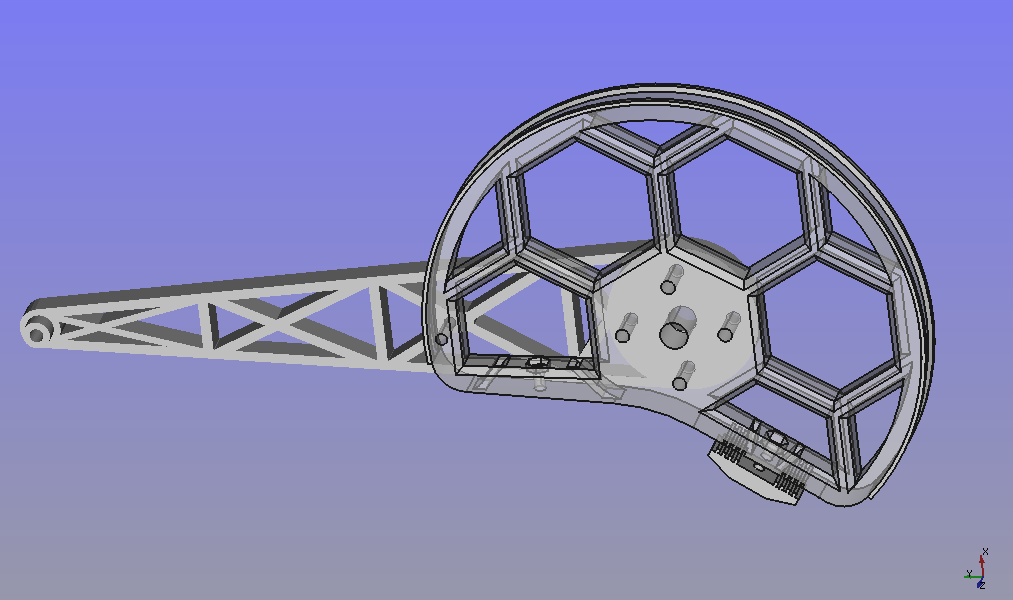











 Matthew James Bellafaire
Matthew James Bellafaire
 Steve Pendergrast
Steve Pendergrast

 RigTig
RigTig
First of all: I very much admire your ambition and work ethic in making this machine, and making it work. Thou art indeed the man.
As for for printing accuracy: You've had a couple years to think about it now, and I want to ask you a few questions please.
Today, how much of the IcePick's printing inaccuracy do you mentally chalk-up to the harder inverse-kinematics sticking you with just ~40 segments per second?
As for tooth-belts, plenty of linear-slide delta-type machines do just fine with tooth-belts, so do you still (partially) "blame" the arms (instead of linear-slides) for its inaccuracy problems?
In general, I'm puzzled as to why there's be so little work being done on delta-arm type machines like this. I'm not calling the whole world stupid, but I AM genuinely confused as to what their inherent deficiencies -- if any -- might actually be. So your comments will be very much appreciated. And thank you.