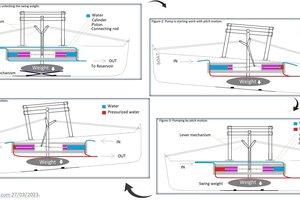
Tidal force on a floating object has two elements:

1) Horizontal force: This is a one-directional force creates by tidal flow/current.

2) Vertical force: Is a bidirectional force creates by tidal waves with gravity.

Tidal horizontal force (and with others external any kind of wind forces) on a floating object can be opposed by anchor it properly (by using minimum four horizontal/ long-distance anchors) so that the vertical force remains almost the same. This vertical force is useful and it can be very much useful as easily increase this vertical force by “Archimedes Principle” (by increasing the size of the object). This bidirectional vertical force is very much suitable for pumping purposes. By installing pump protected by RCC structure, using the vertical upward force of the wave on an anchored floating object continuously sufficient water pumping possible for hydropower station and or desalination.

CALCULATION

Consider a piston cylinder, diameter Dc = 10 m. and     cylinder height ≥ maximum wave height. So the cross section area of cylinder

Ac = π*(Dc)²/4 = π*(10)²/4 m² = 78.54 m² …………………...….(1)

Let, wave heightis 3 m. So the piston can move 3 m.        

i.e. active length of cylinder Hc = 3 m.

If the piston is connected with a floating object then due to a tidal wave the amount of wáter will pump is

Q = Ac*Hc per wave = 78.54 X 3 m³/wave = 235.62 m³/wave

If the wave period is 10 seconds,^[2]

Then Q = 235.62 m³/10 sec = 23.56 m³/sec ……………….(2)

Consider a floating ship of displacement tonnage 10,000.

(i.e. total weight of the ship is 10,000 ton).

According to Archimedes’ principle buoyant force (vertical upward force) on the floating ship due to the tidal wave is ≥10,000 ton force, i.e. V_F ≥ 10,000 ton force.

Let, V_F = 10000 ton force

=  98067.1kN……………………………………...(3)

If this force acting on the piston then, Pumping pressure

P_pump= Force/Area = V_F/A_C

               = 98067.1/78.54 kN/m²  [by eqⁿ (1) & (3)]

             = 1248.63 kN/m²

As measured by a U-tube manometer, 1kN/m² pressure can create a water head 0.102 m.^[3]

Then for Pumping pressure P_pump=1248.63 kN/m², water head

H_head = 1248.63*0.102 m = 127m,

Consider head loss 13 m, then waterfall height

H = 127-13 = 114m.  ………………………..………….(4)

From formula to calculate hydropower, Generating power (P_gen) ^[4]

P_gen = Q*ρ*g*H*η watt, ……….(5)

Where,             Q = flow rate in m³/sec. [=23.56 m³/sec         eqⁿ (2)]

                        ρ = water density in kg/m³    (sea water 1020 kg/m³)^[5]

                        g = acceleration of gravity in m/sec²      (9.81m/sec²)

                        H = water fall height in meter. [=127m          eqⁿ (4)]

                        η = global efficiency ratio.          {let here 0.8}     (Usually between 0.7 and 0.9)

Then eqⁿ (5), Generating power

P_gen = 23.56*1020*9.81*(114)*0.8 watt,

               = 21,500,954 watt

              ...