-
Better sorting
09/25/2022 at 02:23 • 0 commentsThe new version is here : YAMS_20220925_2.tgz
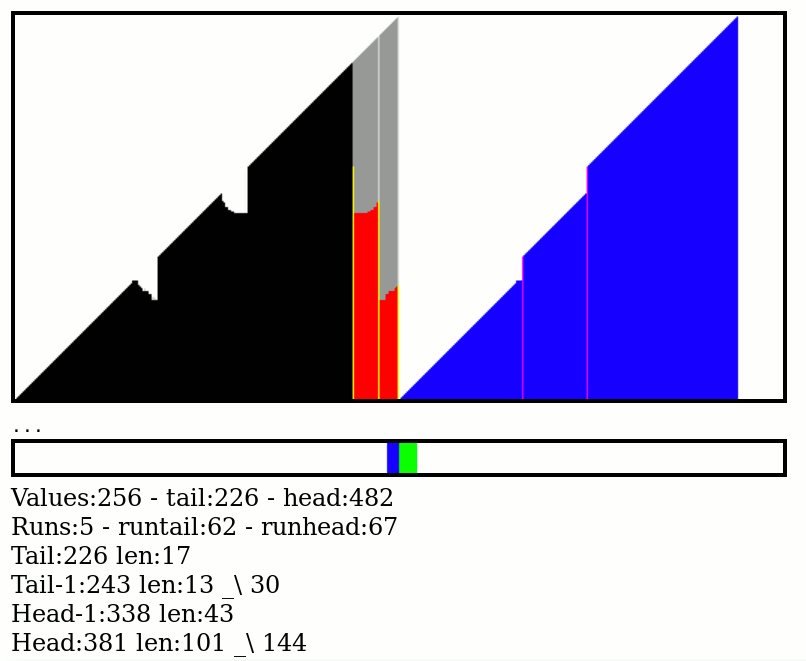
I added a new counter to help measure the efficiency of the algorithm : I accumulate the sizes of the merged runs. The worst case scenario should be the COMB test pattern that has 128 runs of 2, making 256× log2(128) = 256×7=1792 reads and writes total.
Apparently the algorithm is more efficient (with a lower accumulated score) when all the data are processed at once, and not progressively: the progressive reduction of the data also reduces the choices and the opportunities to merges the smallest runs first. A better heuristic is needed but for now, the progressive merging is disabled, I have run the numbers and they are less favourable than straight bulk merging.
The last log Choosing the next move has been tested and debugged, and it works pretty well. The whole thing is starting to take shape now and it looks good.
-
Choosing the next move
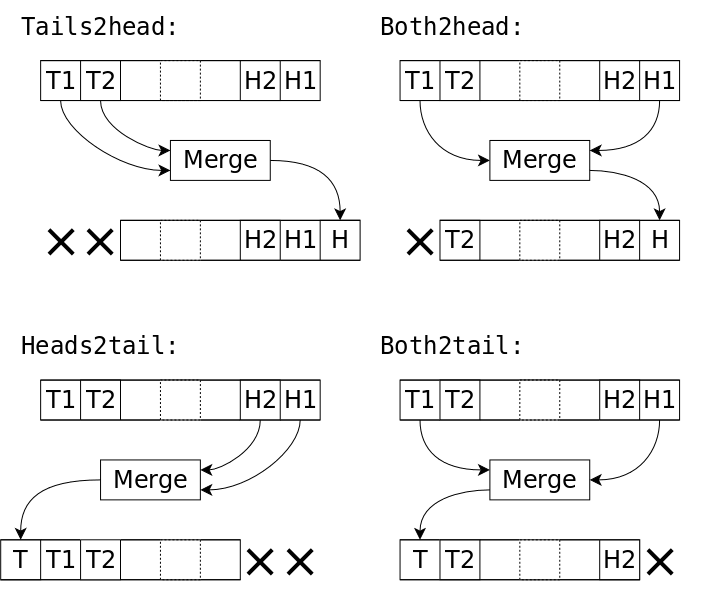
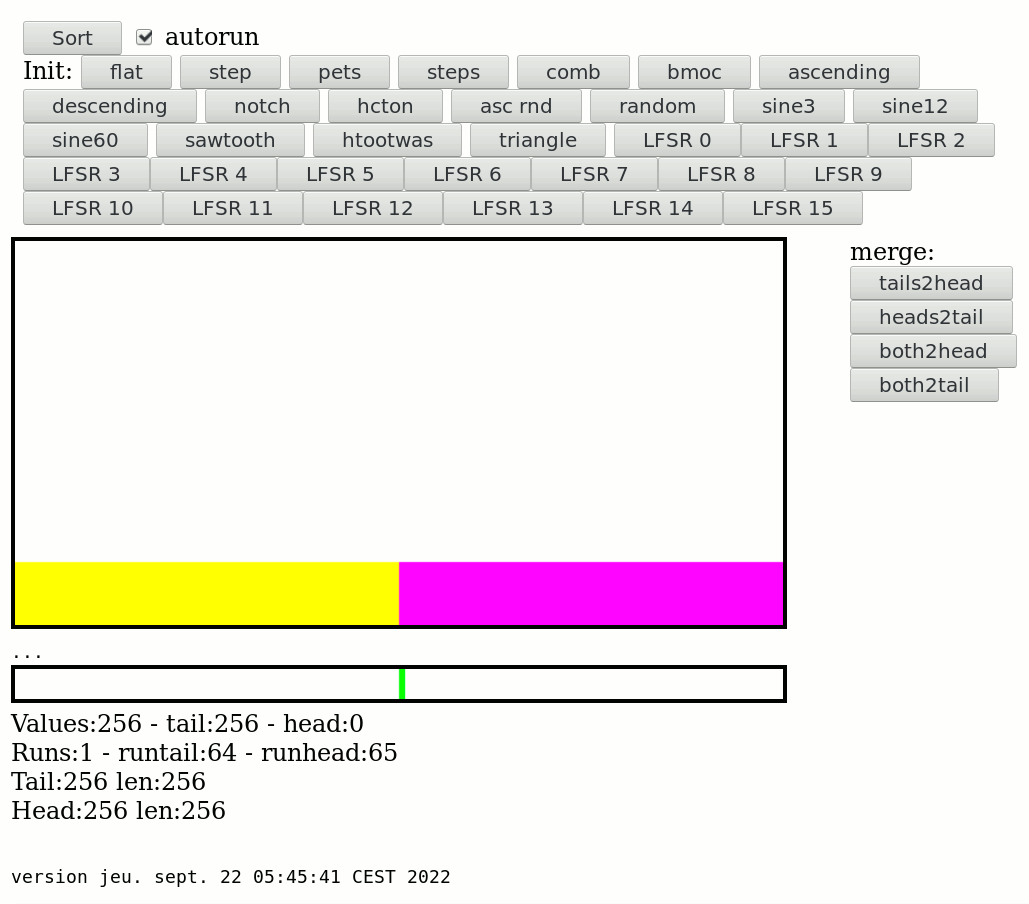
09/24/2022 at 07:30 • 0 commentsYAMS can execute 4 types of merges :
- tails to head
- heads to tail
- both to head
- both to tail
![]()
Of course if they are called in random order, the data will be sorted anyway but it wouldn't be efficient, likely close to O(n²). So this is how to use them more efficiently.
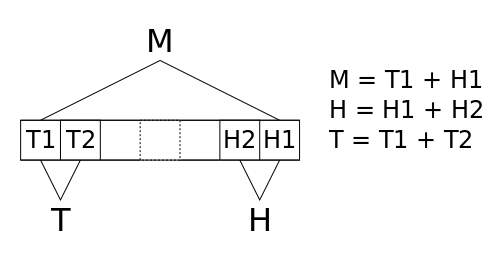
Let's simply consider the final size of all the possible moves : there are 3 sizes M, H and T, the sums of consecutive pairs of runs:
![]()
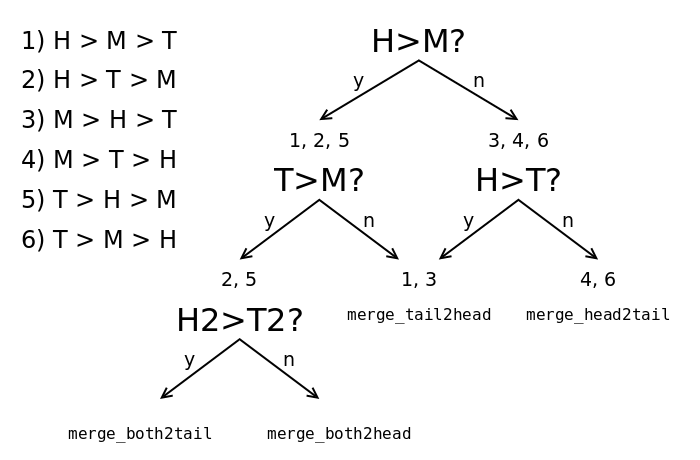
There are 3! = 6 possible permutations when we sort their values (ignoring equal results for a moment) and only 4 moves. 4 tests are enough to decide the move since some combinations are degenerate:
![]()
The algorithm is most efficient by always choosing to operate on the pair that will give the smallest run. In the case M where there are two possible outcomes, it chooses the direction where the following merge will also give the smallest run as well.
-
Landing on all 4s
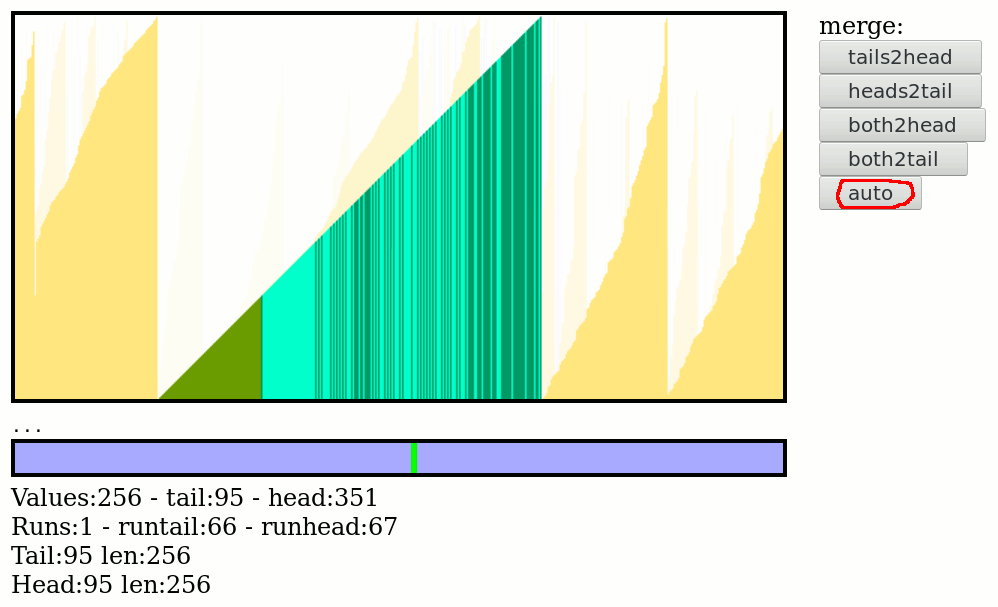
09/22/2022 at 23:24 • 0 commentsSlowly the algorithm takes shape. Here I need to address the special case of the final merge : one of the 4 fusion algorithms must be chosen to ensure that the final block/run sits near the middle of the workspace, or at least not be cut in half by the wrap-around boundary.
To this end, I added the "auto" button so you just pound it until there is only one run left, not cut, ready to be written to a file in a single move. So far the heuristics work well :-)
![]()
That "auto" button is where the rest of the algo will take place, so the final algorithm will just be repeated calls to the corresponding function.
The code is there : YAMS_20220923.tgz.
-
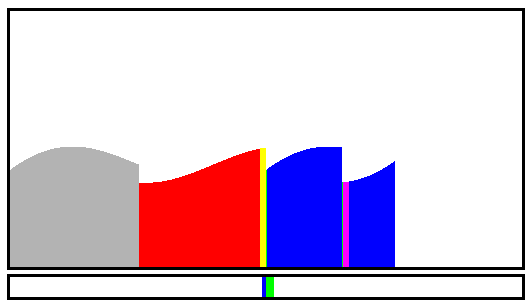
YALO! (Yet Another Little Optimisation)
09/22/2022 at 02:47 • 0 commentsSomething else to consider :
![]()
The blue bloc on the right is made of 3 separate runs. However, since their max/last value est lower than the min/first value of the next run, they could be merged. Which is a potent optimisation for random data, where a non-insignificant fraction of the very short runs could fall in this case. I have to get to work on this too...
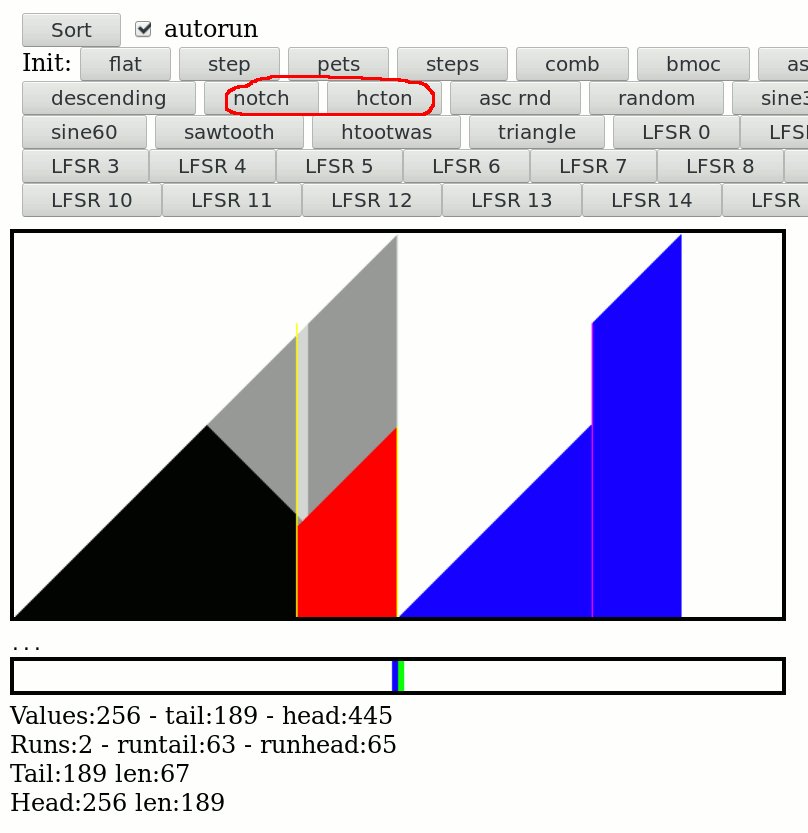
......................
And it works ! These are the new "notch" and "hcton" pattern buttons, the run management system correctly merges those that match the criterion. It's not often but it's still good to have/do.
![]()
It is used from time to time in the random patterns. It is not too heavy but makes it harder to inline the RunHeadPush() and RunTailPush() functions, where the magic goes.
-
Latest.
09/22/2022 at 02:26 • 0 commentsThe latest version YAMS_20220922.tgz is there !
![]()
It seems to work well, particularly since I found a stupid bug in some low-level code.
2 merge strategies exist and can be combined. I now have to make their mirrors to have the whole set of 4 merge strategies.
As an added bonus, you can "draw" your own data with the mouse !
![]()
You even have coordinates though there might be some off-by-ones.
-
Another little optimisation
09/17/2022 at 11:30 • 0 commentsSpeculative write !
I've run the numbers in my head and it must work.
I'm not satisfied with a small part of the run detection algo, which writes the first item(s) over the head and must copy it/them when a decreasing run is detected. It works but it is wasteful because the push then the pop and the push sound wasteful.
The solution is to push at both ends simultaneously, then restore one of the stack pointers when the direction is known, to save a pop with all its pointer-management code.
.
_____________________________________________________
.
.
Voilà ! YAMS_20220918.tgz
![]()
The sequence of identital values gets written to the head and the tail simultaneously. Only one copy is used in the end (by default the increasing run). The size of the playground is sized just right so there is no problem with a duplication of a maximal length run.
.
-
Latest shower thoughts: it's just a dumbed down Solitaire
09/06/2022 at 15:57 • 0 commentsTrying to answer the last questions of the last log, it became more and more apparent that the comparison with the Solitaire card game was worth more than a mere mention. And since the algorithmic part creates too many options, let's play with them, as if they were a game, to get a better "feeling" of the behaviours.
So instead of trying algorithms like one throws spaghetti at a wall, I want to add even more buttons to the interface to perform the algorithm manually. And it would almost look like a Solitaire game in fact. But the flexibility of JavaScript makes it very easy and convenient :-)
So let's start with the new version sort_20220906.html.txt that displays more info, and this helped spot a bug:
![]()
So there would be some data to take decisions by hand. More to come.
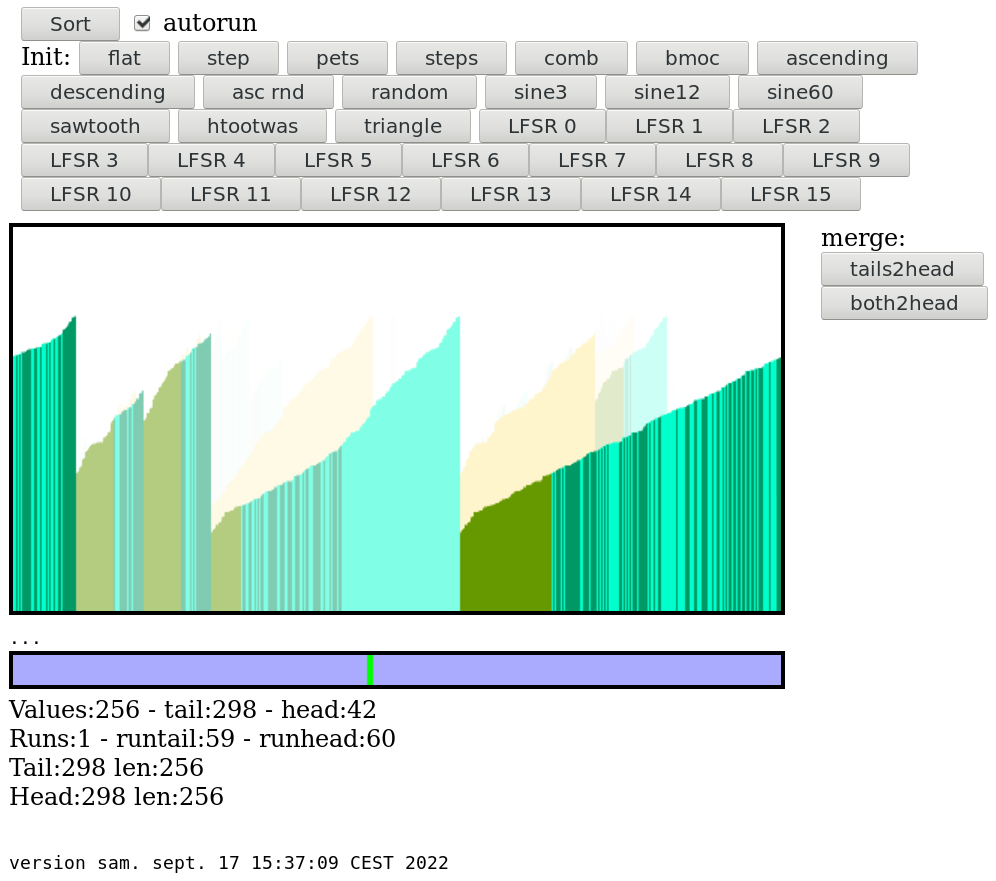
...And sort_20220907.html.txt is working !
Once the runs are pre-sorted, just hit the "tails2head" button and see the magic !
Here is the result for sine12:
![]()
sine60 is pretty nice too:
![]()
The other cases are hypnotising to see working too :-) The comb in particular !
-
Finally getting to the heart of merge sorting
09/04/2022 at 08:05 • 0 commentsThe last log has shown the results of the latest development work, which ensures that input data are correctly pre-sorted into ascending runs as they arrive, at the cost of more than doubling the working area (which is not surprising for a merge sort). In return, there is very little data movement, as the reference frame of the data moves with the data (in the dual-ended circular buffer). So now we can finally focus on merging the runs !
The merge sort idea has a huge appeal because it is so conceptually simple yet efficient. Take two streams of data, and only pick the highest of both values to put in the output stream, and update the pointer to the elected stream. That's all. The implementation spends more code handling the pointers than sorting. There is a lot of headroom for enhancement then.
Modern cores handle many "in flight" instructions at a time, and branch prediction becomes a significant performance bottleneck so the criteria that selected the old, historical, classical sorting algorithms don't hold as before when certain operations were not as costly or cheap. So the idea here is to fill the pipelines with useful work, eventually some might be scrapped but the pipeline should not be flushed as much, data-driven branches are to be avoided. Parallelising operations is also a boost, so several independent instruction threads are interleaved in the pipeline to keep it full, on independent data. That's why processing the runs from both ends is such a great idea and almost doubles the throughput with little effort.
Another aspect to consider is that we could merge/fuse several consecutive runs at the same time. I have decided to limit to 4 runs at once because this makes a total of 5 pointers and counters to keep in the register set, which is tight if you have only 16 registers. Keep some room for the stack pointer & frame, PC and a few other housekeeping variables, and your register set is saturated...
If you can do more, you can do less. What is less than a merge operation? A move operation ! And inbetween the 2 and 4 runs version, a 3-runs version is necessary. The whole runsort algorithm contains the 4 versions in decreasing size order because as each run exhausts, it's better to use a smaller version. But all the versions need to remains available for the cases when fewer than 4 runs are available (like sin60 testcase).
The function would look like this:
function merge4(run1, run2, run3, run4, runcount) { switch(runcount) { case 4: // merge 4 runs until one is exhausted // move the exhausted run out of the list // fold! case 3: // merge 4 runs until one is exhausted // move the exhausted run out of the list // fold! case 2: // merge 2 runs until one is exhausted // move the exhausted run out of the list // move the last run return; default: alert("error ! you shouldn't get there"); } }working with a global array of 4 runs woud probably work best. But wait, there's more because in some cases, the sort can only be work "lowest first" and in other cases, "highest first" (when mixing blocks from both ends of the stack). The case that uses runs from only one side can use the faster version that works with both ends of the runs. So that's 3 versions of the same function, we can start from making a simple one, then the reverse, then both combined : merge_low(), merge_high() and merge_both().
Then 2 big questions arise :
- When to merge ? How many runs are to be in store before we decide to merge some ?
- Which and where to merge them ? From which end(s) and to where ?
The last question in particular is complicated because for the first one, we could use a heuristic or some arbitrary numbers. But the other choice can't be as easily handwaved away. For the case where 2 runs can be merged, there are 4 combinations (assuming there are at least 3 runs) :
- merge 2 tail runs to the head
- merge 2 head runs to the tail
- merge 1 head and 1 tail to the head
- merge 1 head and 1 tail to the tail
Which to choose ?
-
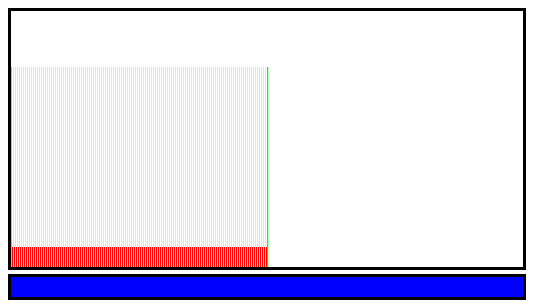
Latest code
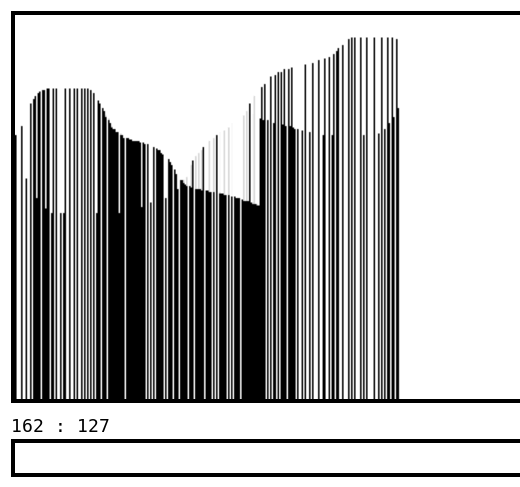
08/31/2022 at 23:45 • 0 commentsThe new file sort_20220831.html.txt is awesome. It implements a lot of the support routines and passes all the tests.
For example it shows the worst case ("Comb") which is exactly the maximum size allocated to the run buffer.
For 256 values to sort, the run "bidirectional stack" needs 128 slots, and the "playground" needs 512 slots. Pretty neat !
I have set the starting point on the "playground" at index 23 but it could be anywhere since all the indices wrap around.
![]()
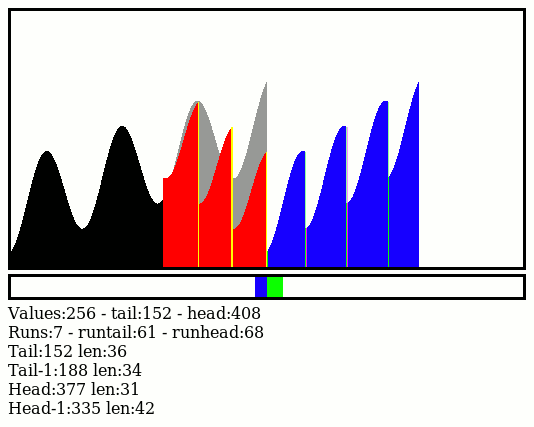
Above, we see the Sine12 test case, showing 4 upslopes (see the green bars at the bottom) and 3 reversed downslopes (blue bar at the bottom right), total: 7 runs.
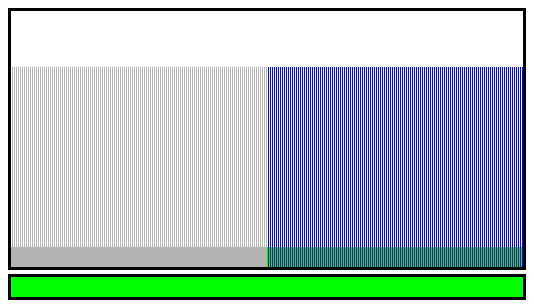
![]()
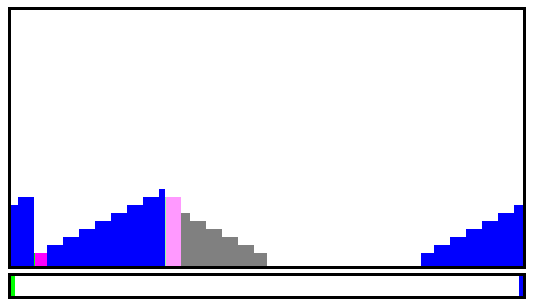
Steps shows 2 runs, one upwards (green bar at the bottom) starting at index 23, then one downwards, but the light pink "undetermined slope" is popped from the head and moved to the tail before accumulating more downwards samples.
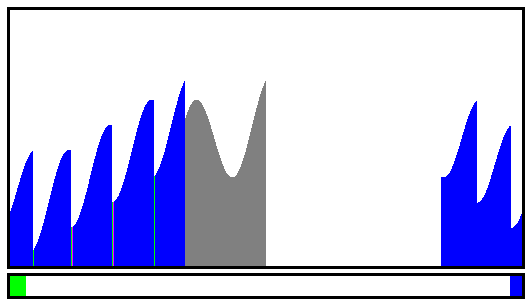
The most crazy cases are still LFSR9, LFSR10 and LFSR14 which have no downslope.
...
Edit
I got a few colors wrong, it's fixed now in the latest code version. Anyway this log was just to prove that the principles I presented previously are totally fine and easy to implement.
Here is the result with the better color scheme and the "origin" in the middle of the range:
![]()
- Red is the data accumulated "in reverse" (at the tail)
- Blue is the data accumulated "forward" (at the head)
- Purple is data accumulated at the head but not sure yet if it's going up or down
- Green is the very first item in a run, so it's very undertermined.
- Yellow is undetermined/horizontal block that is moved from the head to the tail.
- Grey is just some original data that was not yet overwritten (just as a visual reminder, since the data is copied before to a temporary buffer)
The goal is to minimise the yellow areas and the new organisation "dual-ended stack" cuts a lot of unnecessary moves compared to the original idea.
![]()
The "comb" dataset is the worst case that saturates the run buffer but by definition it can not saturates because the smallest runs can be 2-long. One exception is at the very end, with a run of 1 but the buffer's size is a power of two, and to get the 1-long run, at least one other run must be 3 or a larger odd number. QED.
There is one green bar because since it's the only data yet, there is no need to move it :-)
The initial conditions of the comb matter because here is what it does when the data stream start with the lower value:
![]()
Since the first run is "up", the remaining are "up" too and the stack extends to the head. The number of runs does not change though and the runs buffer is totally full yet not overflowing.
-
All in place
08/31/2022 at 21:21 • 0 commentsAs I'm coding the new version of the algorithm, I realise that I could implement a different approach, and I will probably do it when I can.
The canonical algorithm favours "in place" sorting, which the current version doesn't do (I use a stream of data as a source, not a whole block). The current algo does not need too much adaptation to process an existing block that is already in the "circular playing field" though the efficiency/speed/optimality might be a bit less. It might be a bit simpler though since the runs could be detected progressively and require less room (which is great because the algo uses 2× storage space).
- Get your block of data, filling a whole buffer.
- Double the size of that buffer and use circular (wrap around) addressing.
- Now detect the 4 runs from the tail and from the head. That makes two 4-deep stacks.
- Select which runs to merge and where.
- loop to 3 until there is only 1 run.
I think I get the idea but it will be better once I can make a video about it :-)
The drawback is that for random data, the tail and head will progressively have longer and longer runs while the middle will still be quite random. The reverse happens in the current version that inserts data one by one, merging runs progressively into larger and larger runs, while the more random data appears on the edges.
Anyway this alternative approach is worth a try !
YAMS Yet Another Merge Sort
There are already so many sorting algorithms... So let's make another!
 Yann Guidon / YGDES
Yann Guidon / YGDES