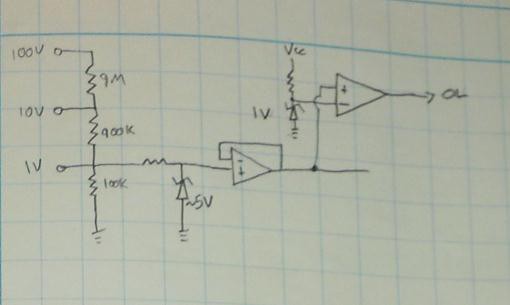
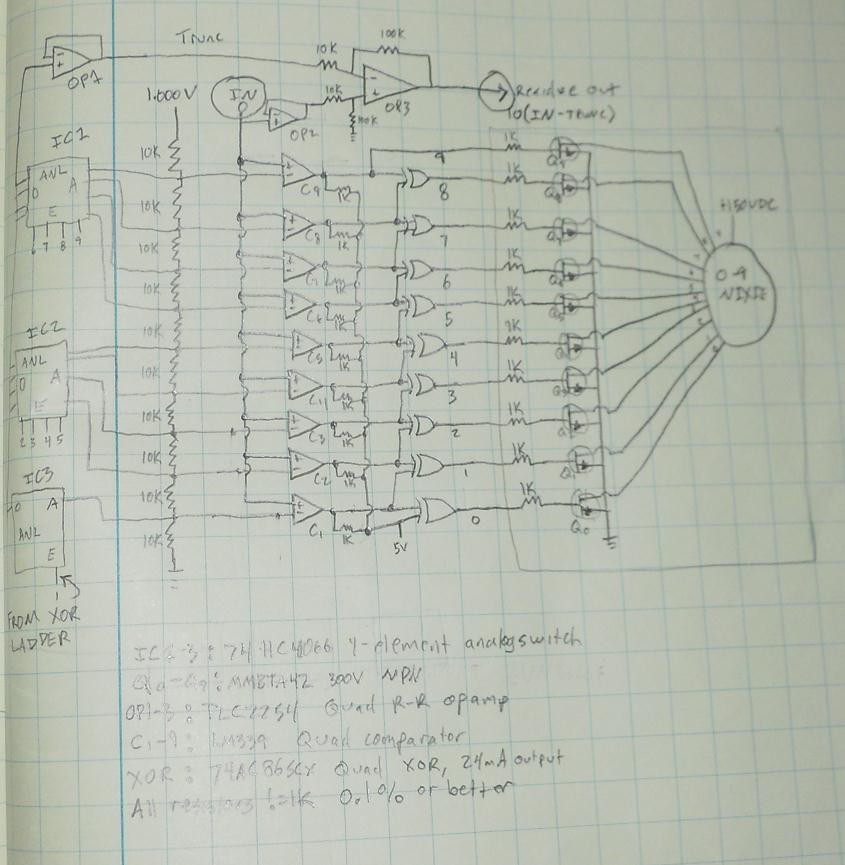
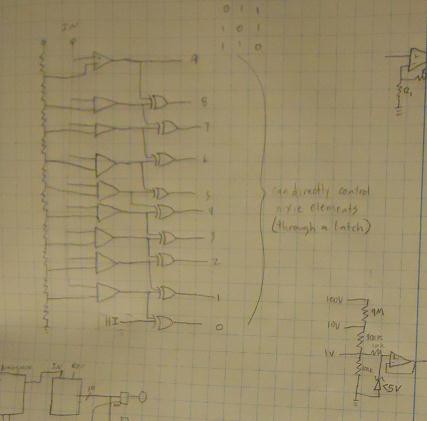
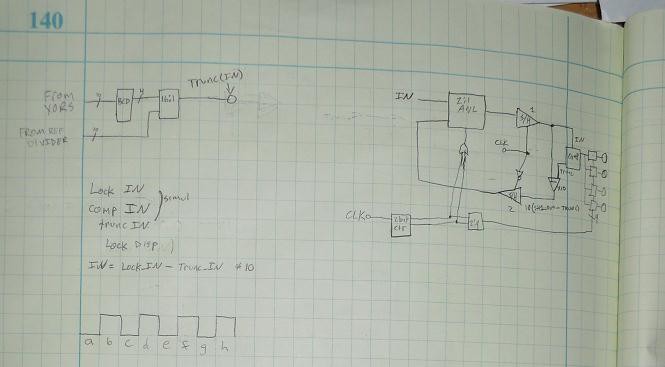
The purpose of this project is to build as diversely functional multimeter as possible, using as little digital electronics as possible. At times it will be required to use something like a single 555 or basic logic, but nothing with nested or combined logic will be allowed (except minimally where it might be required for latching states for a particular type of measurement, or to hold display outputs for readability). No microcontrollers will be used, no self-standing ADCs, no BCD converters, nothing. As much as possible what can be done with just analog circuits (opamps, etc) and discrete passive components (R, C etc) will be done with them only.
Don't even think about telling me to use an Arduino. You will be slapped.
State-Based Nixie Digital Voltmeter
A digital voltmeter built without any microcontrollers or integrated ADC chips. Based entirely around discrete logic and comparator ICs.
 kittan
kittan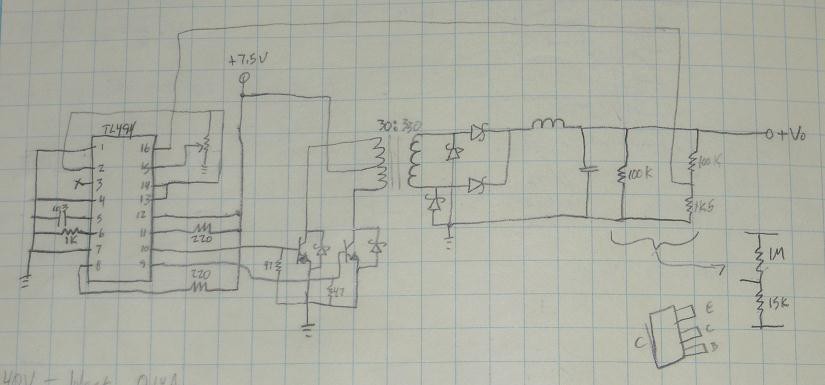


 John Duffy
John Duffy
 James Wilson
James Wilson
 NNNI
NNNI
 Jonathan Bruneau
Jonathan Bruneau