This ALU ( Wikipedia: ALU ) could be used as a building block of a homebrew CPU.
It has not many components. It happens to fit on a one square inch PCB !
It could have been made smaller, using IC's that can only be soldered under a microscope, but it uses SO14 and SO16 IC's that are much easier to mount.
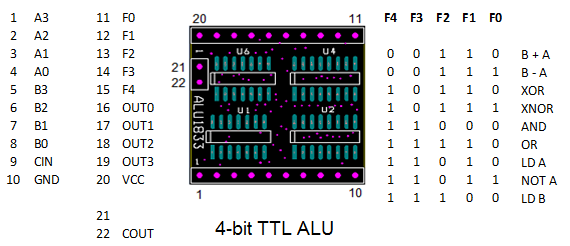
The square PCB has two rows of header contacts, with GND and VCC in the corners. That should sound familiar. This is the I/O:
- 4 inputs A
- 4 inputs B
- 4 outputs
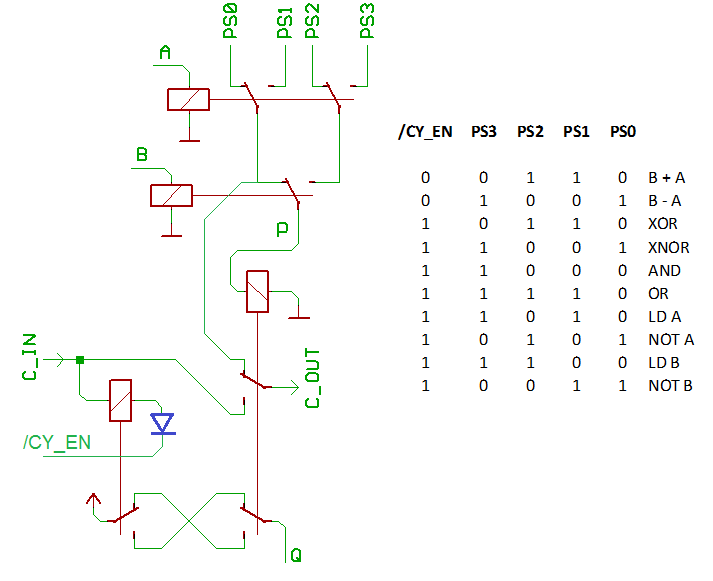
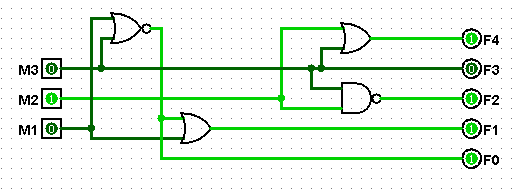
- 5 function select inputs
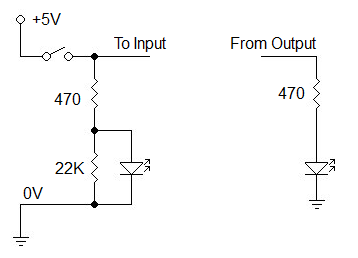
- carry-in and carry-out
Unfortunately, together with the power lines it is 21 signals, just too much for the two 10-pin headers. So the carry-out was banned to an extra 2-pin header on the left side.
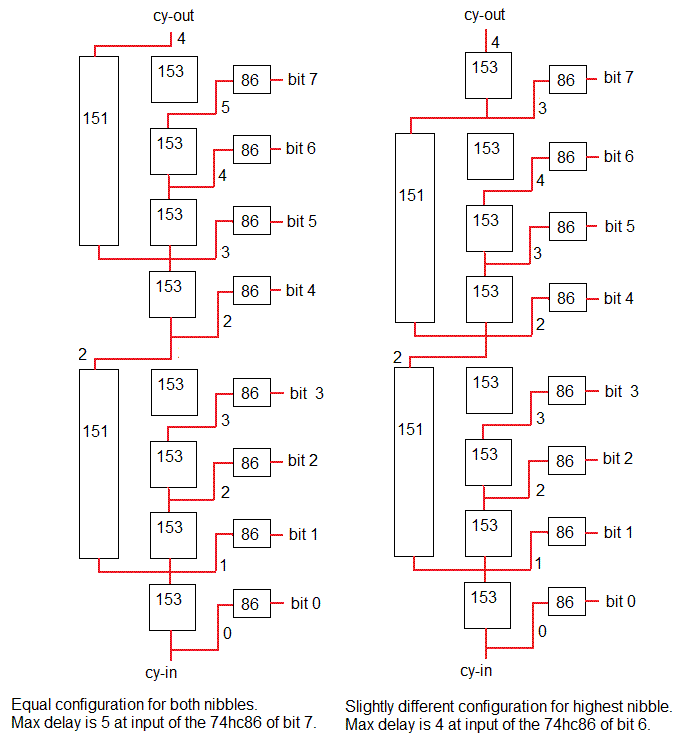
The carry-out is quite fast, the signal from carry-in has to pass only 2 IC's (U2 and U7), giving a theoretical worst case propagation time of 23+17 = 40 nS (Texas Instruments datasheet, Vcc 4.5V, 25 degrees). It can be made faster by using a faster logic family.
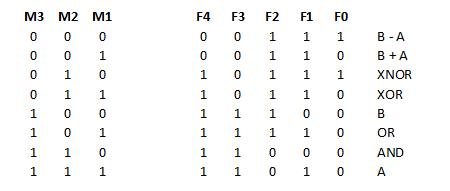
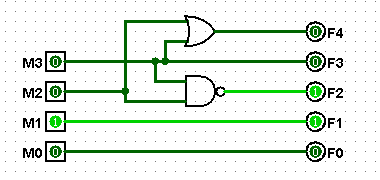
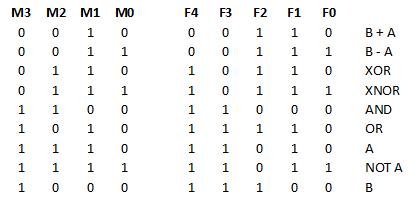
The meaning of the 5 function inputs is given on the schematic (One of the logs shows how to reduce this to 3 signals). The function encoding is not compatible with the 181. Note that for subtraction, the carry input must be "1", just as with the 181. For logic instructions, the carry input must be "0" (the carry output is always "0" for logic instructions).
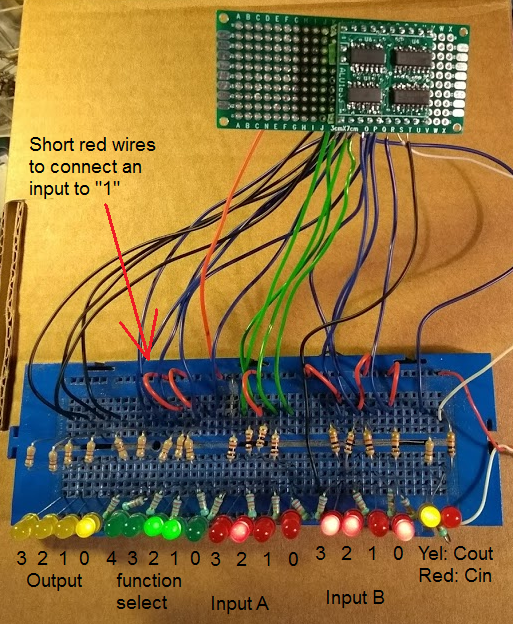
The design has been successfully simulated in Logisim (the Logisim design is in the files section). It has also been built and it works great !
If you are interested in ALU design, check my DCTL Transistor ALU and the relay-based ALU in my RISC Relay CPU.
I will use the logs to explain the circuit (for best results, read the oldest log first).










 Lilia Lobato
Lilia Lobato
 zpekic
zpekic
Fortunately, internal carry propagate cases are wired to MUX inputs and not to select inputs. Replace HC153 with CBT3253 transmission gate multiplexers of the same pinout to eliminate combinatorial ripple. 74CBT MUX are 6nS to setup, 5 ohms, and 250pS to propagate. Ditch look-ahead and wire the last bit same as the first three.
https://hackaday.io/project/160506-4-bit-ttl-alu/log/155600-a-relay-alu
Observe how your carry once had a switched path, without reliance on ripple or look-ahead. Thats where I want to return with the CBT logic, to a relay style instant pass-through, not limited in length to four bits.
--edit--
Another important change, bitwise generate and annihilate are not wired VDD, GND. But instead new control inputs allowing the carry chain to borrow, reverse borrow (B-A's borrow), compare equalities and inequalities, or be jammed to a uniform set or clear state for undisturbed logic. No need to disable /OE, wouldn't want final XOR to see an open disabled pass-through.
Lets look at logic controls. You feed three truths, I feed only two. In my case the carry chain can be set or cleared to flip any logic result, so one truth input can be ground without losing any functions. I then sacrifice a few asymetrical functions by merging the middle cases 01 , 10 together and treating as one. But thats optional...
For all differences, each bit is still just a pair of 4way mux on one chip and a pair of whatever XOR you happen to favor. The 8way look-ahead MUX isn't needed.