I suggest reading the posts in chronological order. Many terms are introduced early on and not explained in any detail later. Also, several concepts are evolving as I go.
You can see the posts in order by clicking on the "View all # project logs" button and then sorting by oldest.
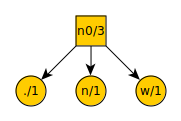
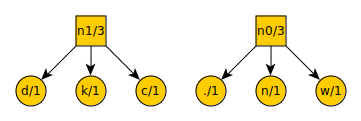
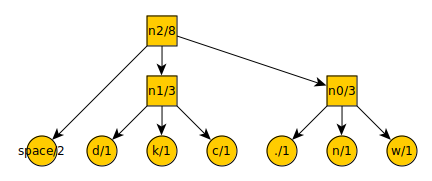
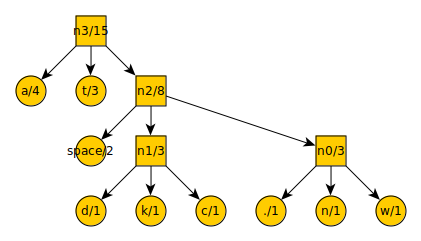
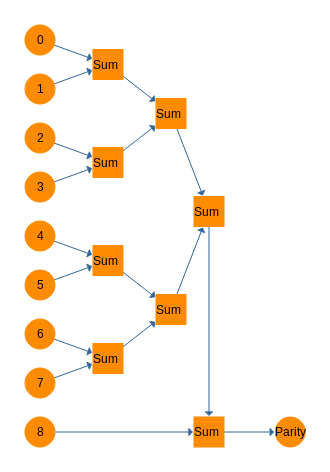
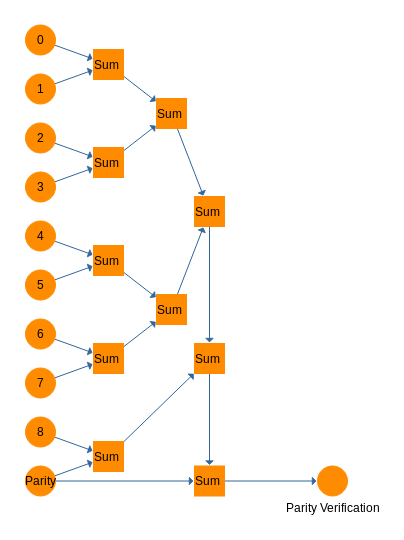
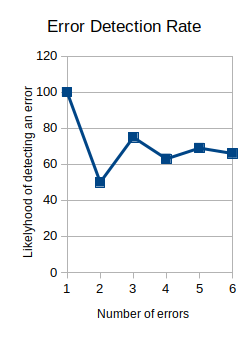
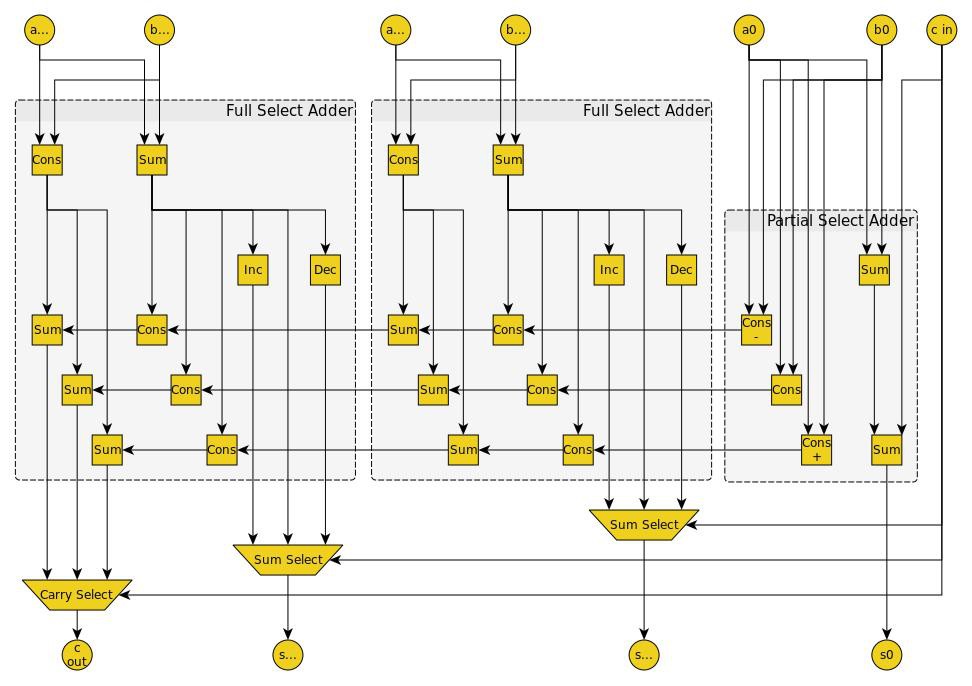




 Tim
Tim
 Yann Guidon / YGDES
Yann Guidon / YGDES
I've been working on an emulator for a ternary computer here:
https://github.com/tedkotz/ternary
It has a debug monitor mode that it runs in right now so you can single step through hand assembled programs. and I'm working on throwing together an assembler for it.