I decided to build a FP with 8-bit exponent and 9-bit mantissa (and with no NANs, infinities, denorms or rounding).The
sum of the bit-lengths (plus one sign bit) means that the FP number
fits into a 18-bit M4K block word on the CycloneII FPGA. The 9-bit
mantissa means that only one hardware multiplier (out of 70) is used for
the floating multiplier. The exponent is represented in 8-bit offset
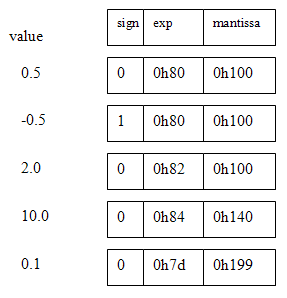
binary form. For example 20=128, 22=130, and 2-2=126. The mantissa is represented as a 9-bit fraction with a range of [0 to 1.0-2-9]. A sign bit of zero implies positive. The Verilog representation is {sign,exp[7:0],mantissa[8:0]}.
Denormalized numbers are not permitted, so the high-order bit (binary
value 0.5) is always one, unless the value of the FP number underflows,
then it is zero. No error detection is performed and there is no
rounding. There are no NANs, infinities, denorms, or other special cases
(which make little sense in a realtime system anyway). Some example
representations are shown below.
Five operations are necessary for floating DSP. They are add,
negate, multiply, integer-to-float, and float-to-integer. Negate is
easy, just toggle the sign bit. The integer conversion algorithms are
necessary because the audio and video codecs are integer-based. Outlines
for the functions are below. Finally, the modules were tested by
building IIR filters. The SOS filters shown below validated the
performance of the floating point. An article written for Circuit Cellar Magazine describing this floating point is available.
Multiply algorithm:
- If either input number has a high-order bit of zero, then that input is zero and the product is zero.
- The output exponent is
exp1+exp2-128orexp1+exp2-129. If the sums of the input exponents is less than 129 then the exponent will underflow and the product is zero. - If both inputs are nonzero and the exponents don't underflow:
- Then if
(mantissa1)x(mantissa2)has the high order-bit set, the top 9-bits of the product are the output mantissa and the output exponent isexp1+exp2-128. - Otherwise the second bit of the product will be set, and the output mantissa is the top 9-bits of
(product)<<1and the output exponent isexp1+exp2-129. - The sign of the product is
(sign1)xor(sign2)
- Then if
Add algorithm:
- If both inputs are zero, the sum is zero.
- Determine which input is bigger, which smaller (absolute value) by first comparing the exponents, then the mantissas if necessary.
- Determine the difference in the exponents and shift the smaller input mantissa right by the difference. But if the exponent difference is greater than 8 then just output the bigger input.
- If the signs of the inputs are the same, add the bigger and (shifted) smaller mantissas. The result must be
0.5<sum<2.0. If the result is greater than one, shift the mantissa sum right one bit and increment the exponent. The sign is the sign of either input. - If the signs of the inputs are different, subtract the bigger and
(shifted) smaller mantissas so that the result is always positive. The
result must be
0.0<difference<0.5. Shift the mantissa left until the high bit is set, while decrementing the exponent. The sign is the sign of the bigger input.
The multiplier takes about 60 logic elements plus one hardware
multiplier on the CycloneII FPGA, while the adder takes about 220 logic
elements. The timing analyser suggests that the purely combinatiorial
multiplier should be able to run at 50 MHz and the adder at 30 MHz or
so.
The integer-to-FP and FP-to-integer conversion routines allow you to specify a signed scale. Going from integer to float, the resulting floating point number is (integer_input)*2scale_input. This feature allows you to convert numbers less than one. Going from float back to integer, you choose the scale you want to bring the floating point number back into a small integer range. The signed integer inputs and outputs are 10-bit, 2's complement format.
Integer to FP:
I assumed 10-bit, 2’s complement, integers...
Read more » Bruce Land
Bruce Land
 SHAOS
SHAOS

My former colleague Pavel Dourbal came up with a fast, approximate multiplication algorithm (paper at https://arxiv.org/abs/1602.07008) that might be of interest here