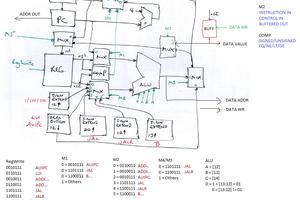
Briefly about architecture and instruction set - it is 8-bit design with 8 registers:
000 - 0 (always zero) 001 - A (accumulator) 010 - B 011 - C 100 - D 101 - E 110 - F (flags and 3 higher bits for jumps) 111 - G (8 lower bits of program counter)
Flags (register F):
bit 7: S - sign (negative result of previous operation);
bit 6: Z - zero (zero result of previous operation);
bit 5: V - overflow (sign overflow in case of add/subtract);
bit 4: C - carry/borrow (borrow is inverted);
bit 3: H - half carry (between nibbles);
bit 2: P10 \
bit 1: P9 - higher bits to set PC in case of jump (reg.G)
bit 0: P8 /
All instructions have 1-byte length:
0xxxxxxx - put 7-bit number into accumulator (A=0xxxxxxx);
10xxxyyy - copy value of register yyy to register xxx (xxx=yyy),
but if xxx is the same as yyy then invert the value
and if xxx=0 then it's subroutines RST and RET;
11oooxxx - ALU operation ooo (see below) with register xxx
(or number), result is stored in accumulator.
ALU operations:
000 - RRC (shift right any register through flag C, res.to A); 001 - RLC (shift left any register through flag C, res.to A); 010 - NAN (bitwise NAND between any register and A, res.to A); 011 - XOR (bitwise XOR between any register and A, res.to A); 100 - ADC (add any register to accumulator with carry C); 101 - SBC (subtract any register from A with borrow /C); 110 - ADI (add 3-bit number to accumulator); 111 - SBI (subtract 3-bit number from accumulator - see below).
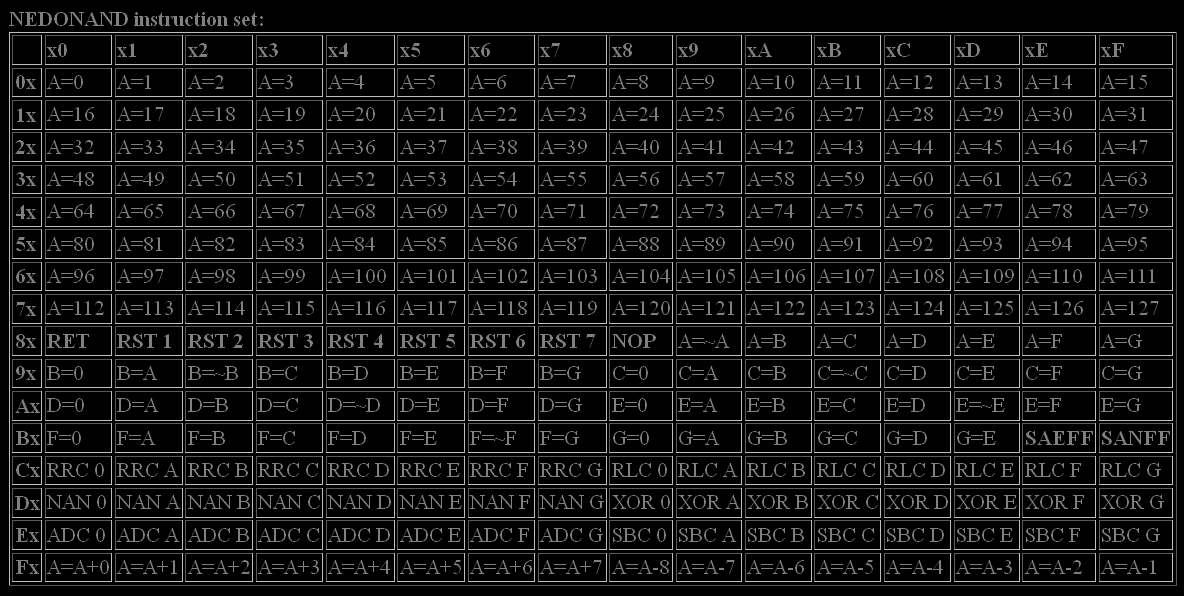
Some comments about opcodes (* if not yet implemented):
| Opcode | Description |
| 00..7F | A=n copy instruction to A (n=0..127) |
| 80..87 | RET (swap + skip) and RST n (prepare F' & G' and swap) * |
| 88 | NOP (instead of A=0 that could be done differently) |
| 89..BD | R1=R2 if R1 and R2 are the same then store inverted value |
| BE, BF | SAEFF (Skip if A is Equal to 0xFF) and SANFF (Skip if A is Not equal to 0xFF) * |
| C0..FF | ALU operation (2nd stage of pipeline is used) |
Aliases:
CLC is A=A+0 (clear flag C)
SEC is XOR 0 (set flag C)
AFF is NAN 0 (store -1 to A)
Note: F=~F and F=G could be changed to memory access A=[DE] and [DE]=A or something like that...
Resets (similar to Intel 8080):
RST1 - call 0x008 RST2 - call 0x010 RST3 - call 0x018 RST4 - call 0x020 RST5 - call 0x028 RST6 - call 0x030 RST7 - call 0x038
RET (0x80) will return control back from RST subroutine (this part is not yet designed), but if called from higher level will behave as HALT (added on 03/26/2016)
All source codes are freely available and trackable through git: GitLab (since June 2018)
You can purchase proven NEDONAND boards on OSHPark: OSHPark/Shaos
Hardware files for Eagle v5.12 and gEDA (pcb) in ZIP archives: Eagle files, gEDA files
 SHAOS
SHAOS




















 Bruce Land
Bruce Land
 Phil Wright
Phil Wright
Страничка в ВК https://vk.com/pluton_tut