Optical system
This 360° camera takes advantage of the optical properties of spherical mirrors. By looking at the mirror beneath itself, an observer can grasp a (deformed) view of the surroundings.
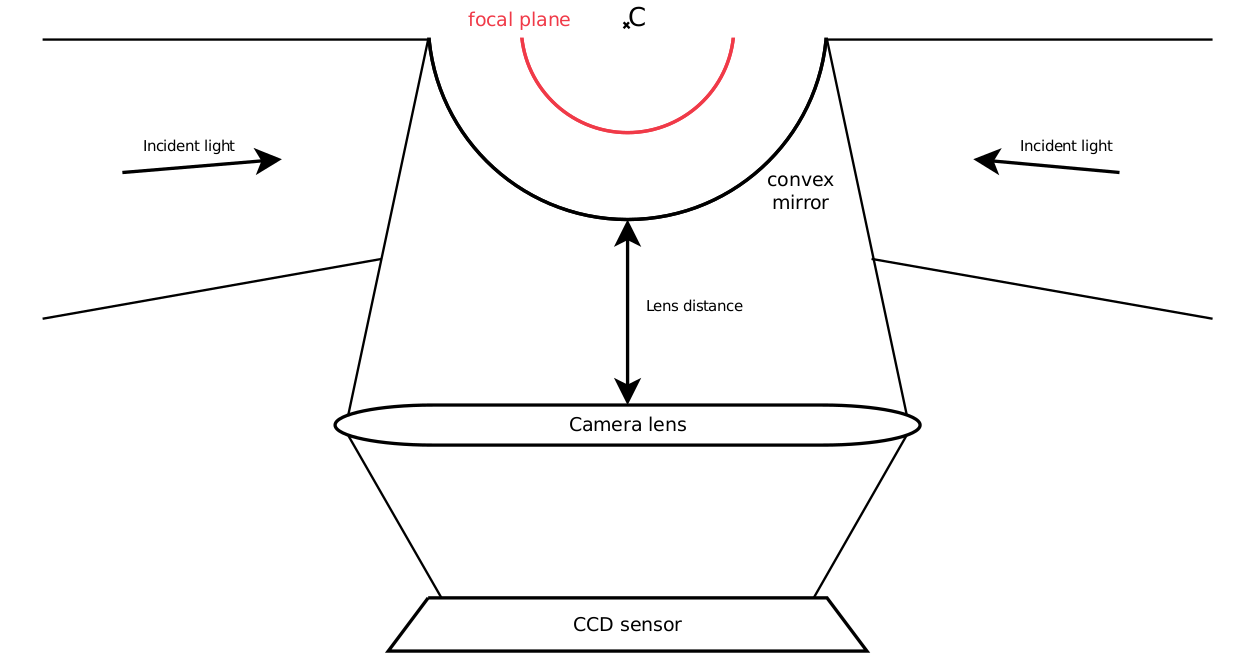
The main approximation of this design is that real observed objects are "far away" from the spherical mirror, meaning that the focal length of the mirror is w[a+]y inferior to the distance from the mirror to the observed objects.
It is not too restricting for useful applications, and virtual images of objects are now considered to be created at the focal plane of the spherical mirror.
The objective of the camera (its lens) is used to focus the virtual images coming from the mirror's focal plane, to the CCD sensor of the camera.
The focal length of the objective is crucial to tune the distance between the camera and the spherical mirror.
Unwrapping
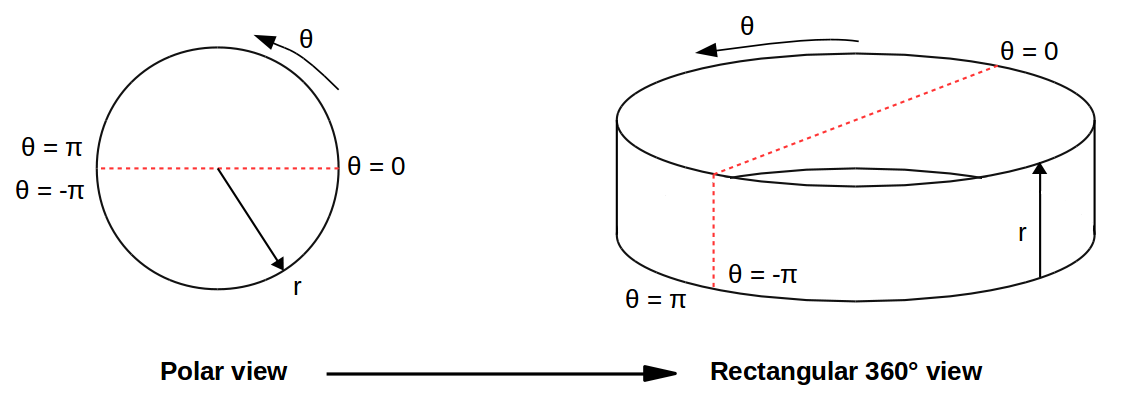
The output of the camera is a "spherical" picture, in polar (r, theta) coordinates. A first processing is needed to unwrap this picture into 360° coordinates.
The most basic unwrapping algorithm maps the polar coordinates to a 360° rectangular ribbon:
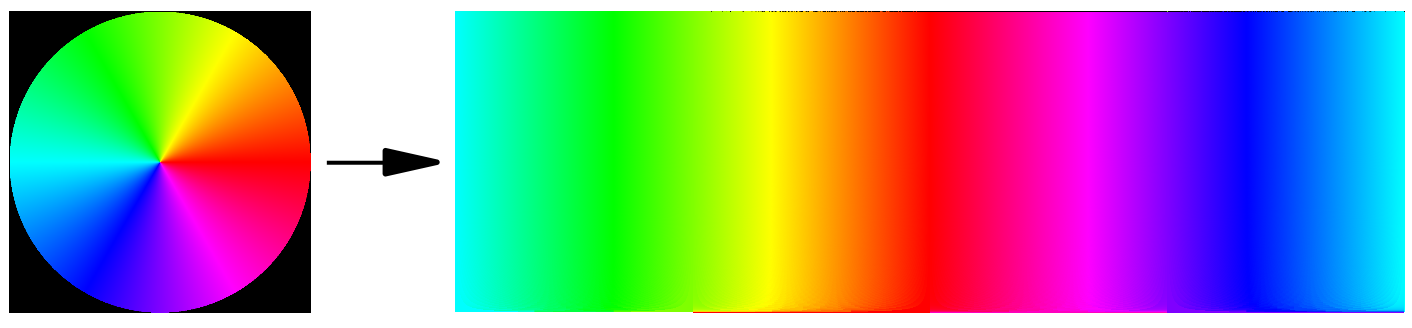
For example, here is the algorithm applied to a color wheel
Wavelet enhancement
A picture can be scattered into its discrete wavelet transform, which holds all the necessary information to describe the image.
The DWT is composed of approximation coefficients, and several levels of detail coefficients:

Some details can be discarded to compress the image like in JPEG 2000.
But the goal of wavelet enhancement is to add levels of details. First of all, the size of the DWT is extended by one level, with no new details coefficients:

[Next is coming soon]
 Alexis Rey
Alexis Rey
 Pavel
Pavel
 AIRPOCKET
AIRPOCKET
 Karri Palovuori
Karri Palovuori