The whole project is built around the STS-5 geiger tube. The 400V needed for the tube are provided by a 555-based step-up converter very common on the internet.
The geiger pulse is then inverted and fed to a monostable 555 to stretch the pulse. The 555 drives through a transistor a buzzer and a led, and the signal is sent to the microcontroller.
The microcontroller is an atmega328p. The geiger signal goes to the ICP1 (input capture for timer 1) pin, which stores the current 16 bit timer1 value in a register and generates an interrupt. When the interrupt is raised, the microcontroller takes the value from the capture register and sends it as two raw bytes over the serial to the computer.
Ent test was taken on a two-day sampling and showed no significant problems in the randomness.
 valerio\new
valerio\new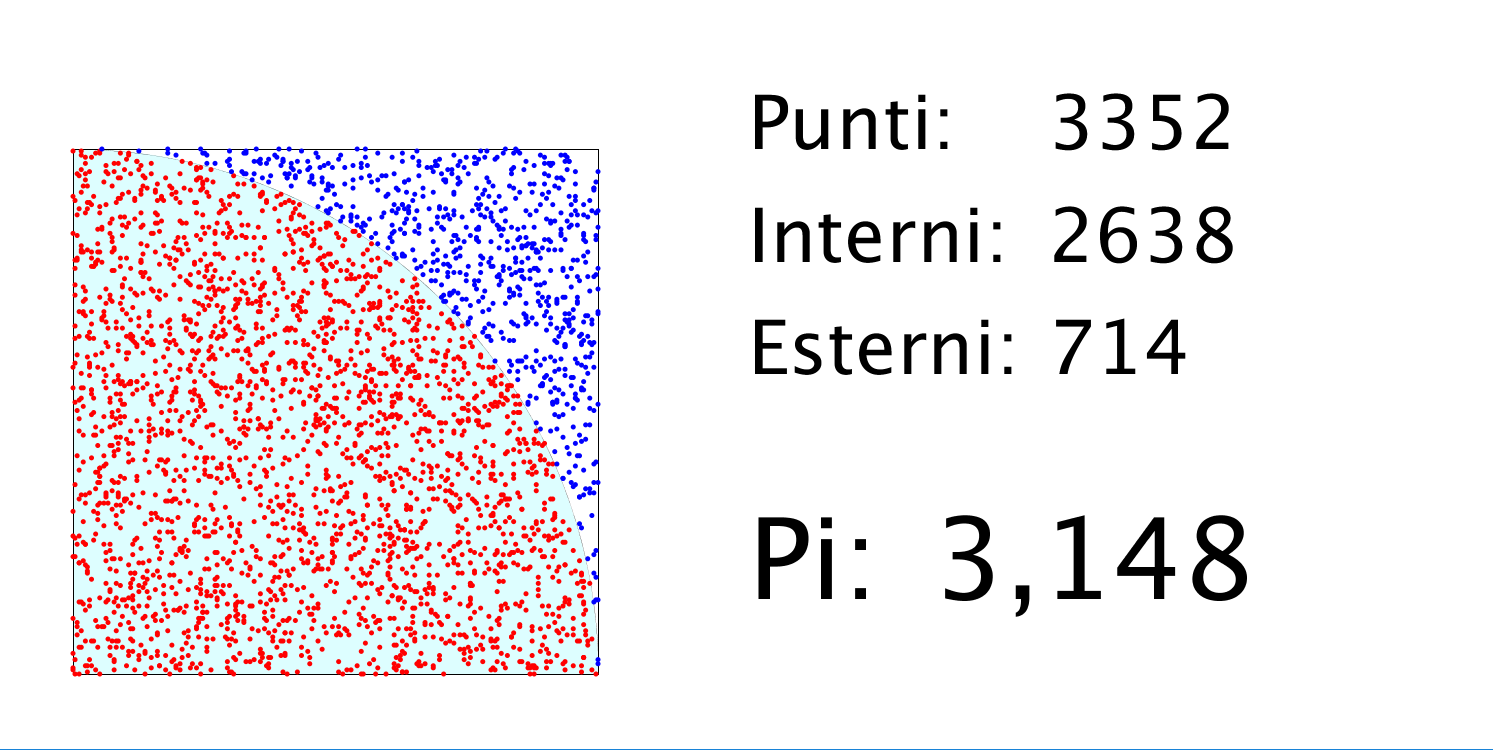





 Mark VandeWettering
Mark VandeWettering
 mateusz.kolanski
mateusz.kolanski
 Eric Herbers
Eric Herbers
 Sagar 001
Sagar 001
HAHA. I want one. NOW! Even if the background noise is stronger than the bananas radiation, who cares.
This will give people plenty to talk about at a party. It even has a banana for scale!