Yann Guidon / YGDES
Let's simply start with a simple algorithm pointed to by Wikipedia and that seems to have been widely used :
pseudo-LRU
two-way set associative - one bit
indicates which line of the two has been reference more recently
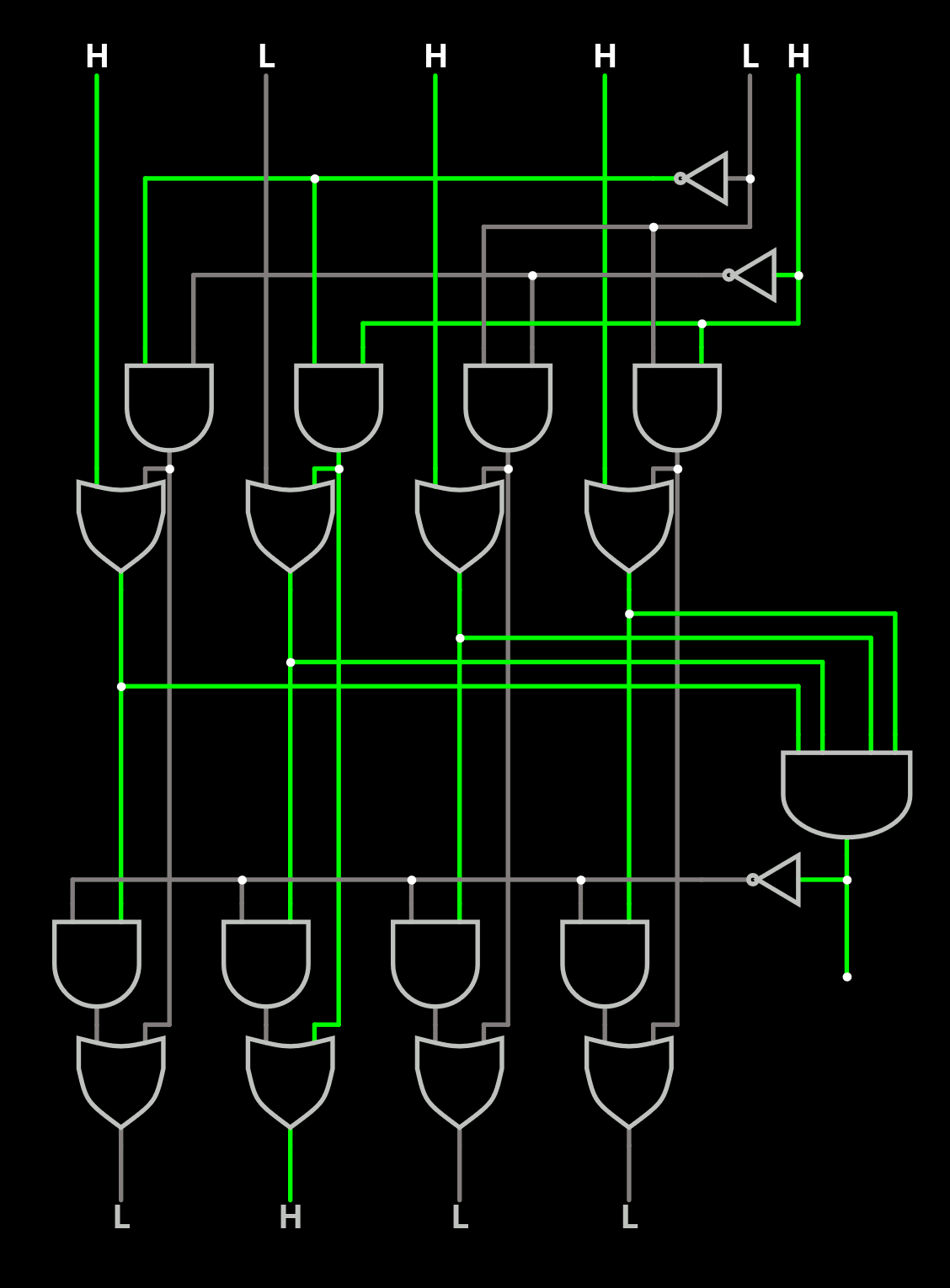
four-way set associative - three bits
each bit represents one branch point in a binary decision tree; let 1
represent that the left side has been referenced more recently than the
right side, and 0 vice-versa
are all 4 lines valid?
/ \
yes no, use an invalid line
|
|
|
bit_0 == 0? state | replace ref to | next state
/ \ ------+-------- -------+-----------
y n 00x | line_0 line_0 | 11_
/ \ 01x | line_1 line_1 | 10_
bit_1 == 0? bit_2 == 0? 1x0 | line_2 line_2 | 0_1
/ \ / \ 1x1 | line_3 line_3 | 0_0
y n y n
/ \ / \ ('x' means ('_' means unchanged)
line_0 line_1 line_2 line_3 don't care)
(see Figure 3-7, p. 3-18, in Intel Embedded Pentium Processor Family Dev.
Manual, 1998, http://www.intel.com/design/intarch/manuals/273204.htm)
note that there is a 6-bit encoding for true LRU for four-way set associative
bit 0: bank[1] more recently used than bank[0]
bit 1: bank[2] more recently used than bank[0]
bit 2: bank[2] more recently used than bank[1]
bit 3: bank[3] more recently used than bank[0]
bit 4: bank[3] more recently used than bank[1]
bit 5: bank[3] more recently used than bank[2]
this results in 24 valid bit patterns within the 64 possible bit patterns
(4! possible valid traces for bank references)
e.g., a trace of 0 1 2 3, where 0 is LRU and 3 is MRU, is encoded as 111111
you can implement a state machine with a 256x6 ROM (6-bit state encoding
appended with a 2-bit bank reference input will yield a new 6-bit state),
and you can implement an LRU bank indicator with a 64x2 ROM
Of course the 1998 link on the Intel website has long been broken but this gives us a first approximation :
- 2-sets uses 1 bit. This can't be more simple or easy and the logic is truly minimal. Go for it everytime you can :-)
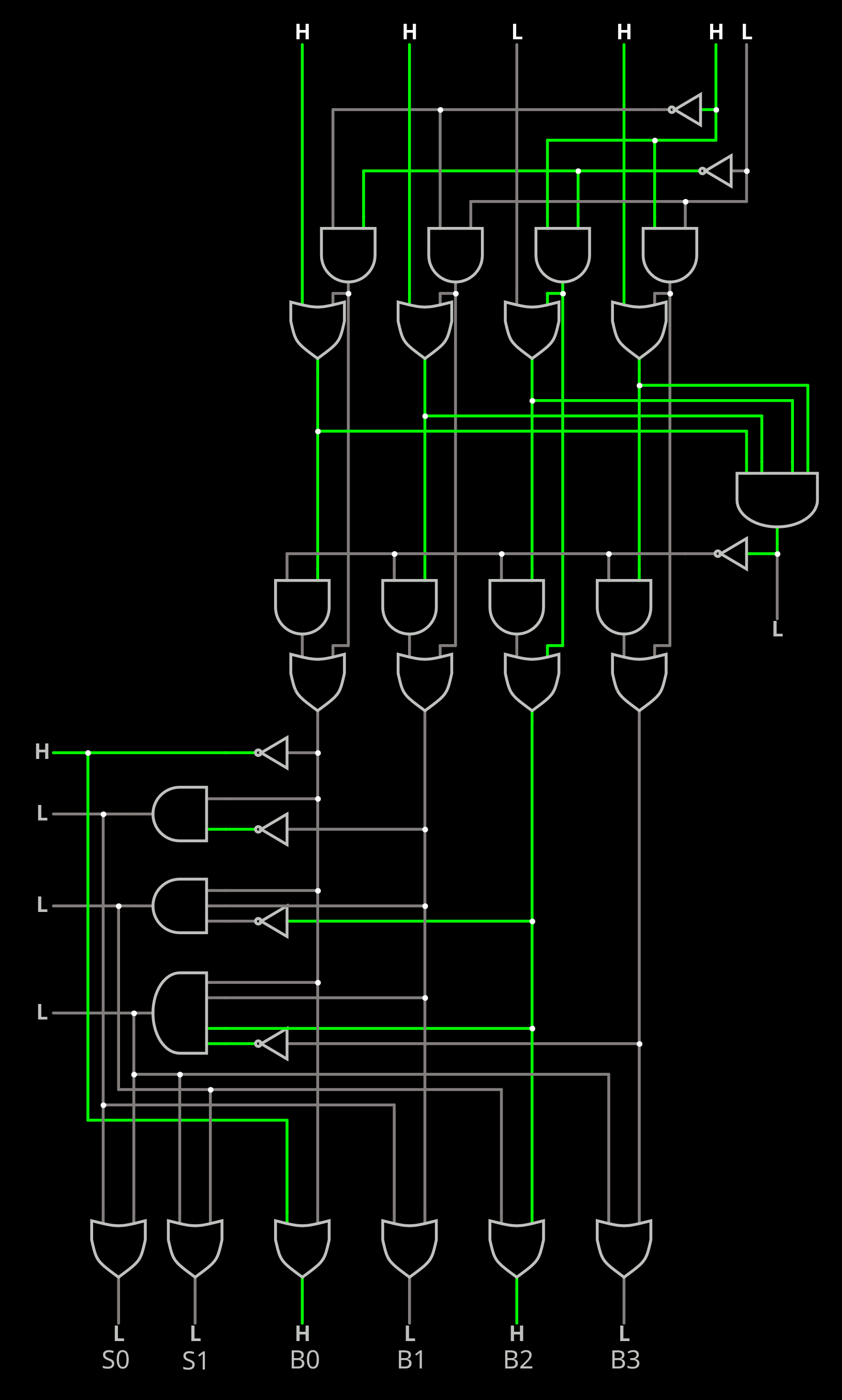
- 4-sets is more complex. There are only 3 bits if pseudo-LRU is good enough for you, but true LRU now has to be distinguished and grows as N!, so you'll need 6 bits and a 256-bits ROM.
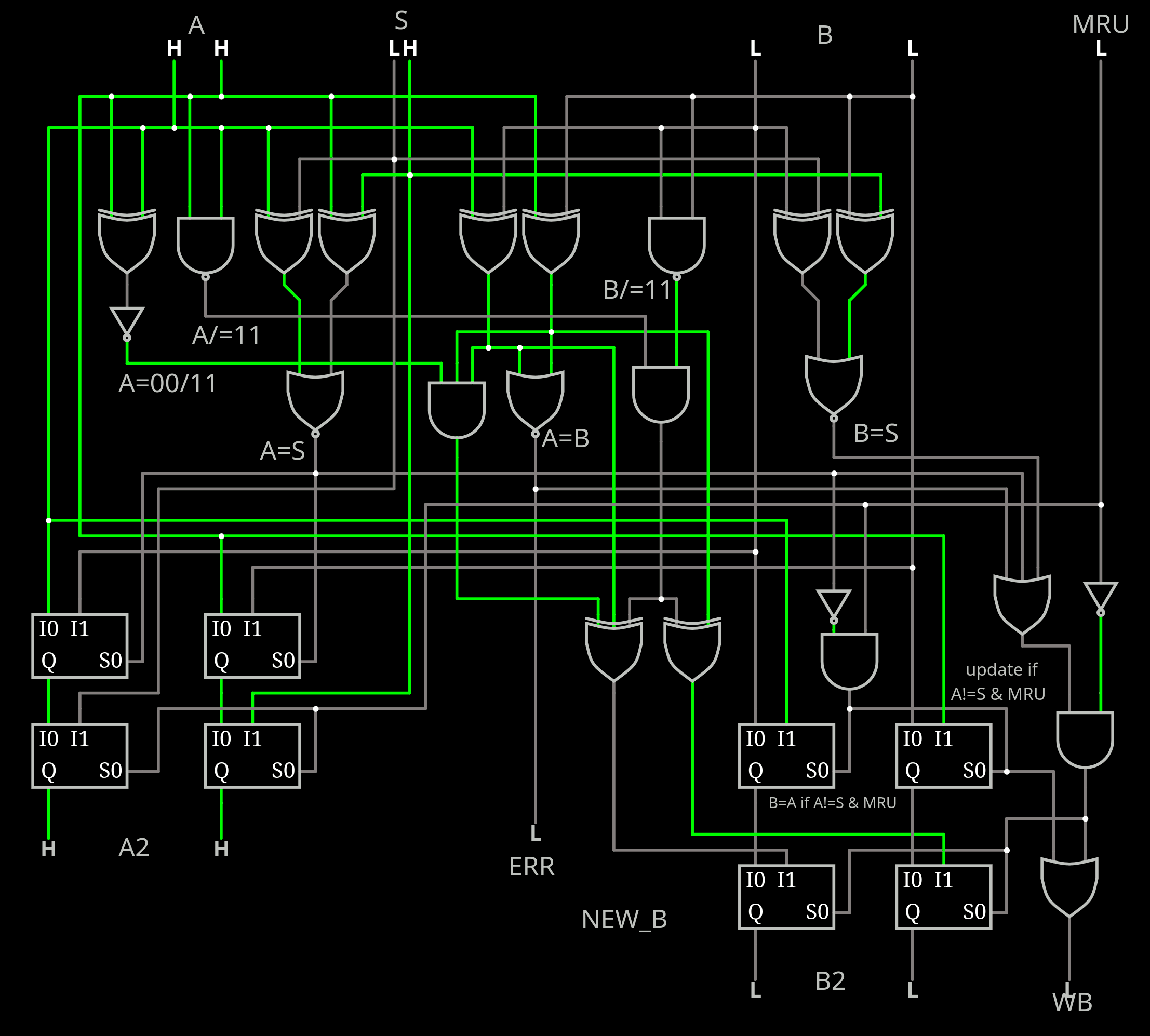
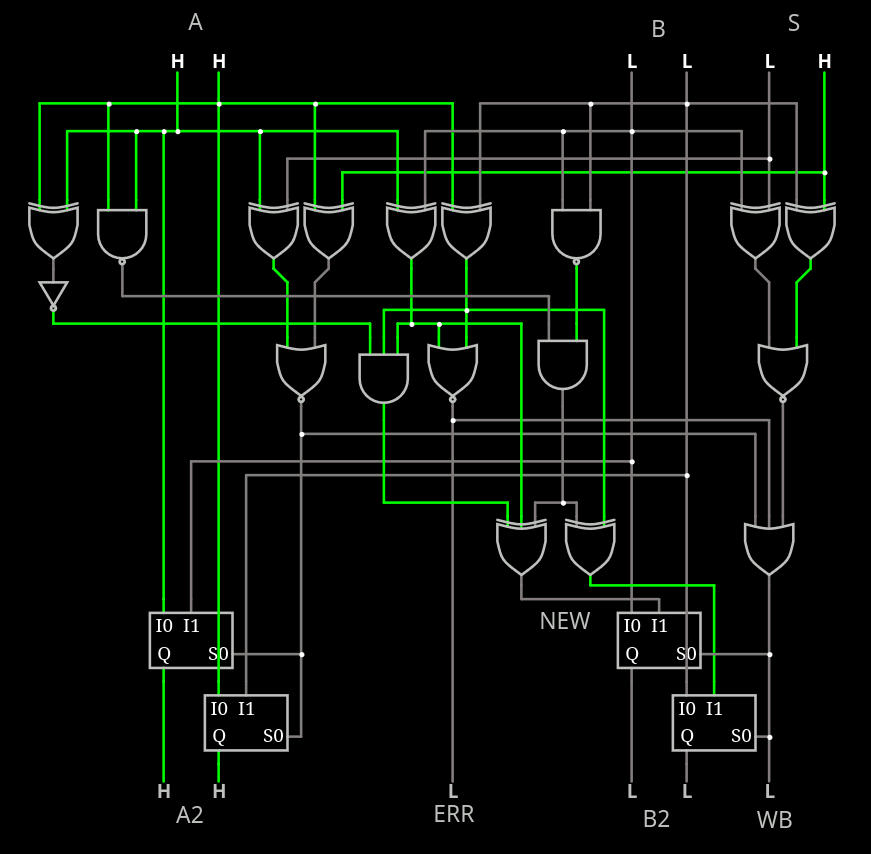
How can one build larger systems ?
Wikipedia lists many strategies but it is desirable to get "most" of the true-LRU benefits without the size, time and costs.
Logs:
1. 4-LRU
2. 4-way Pseudo-LRU
3. PLRU4
4. MRU mode
5. The other LRU
6. MRU in L1
7. Hit or miss
8. More complete myLRU
9. .
10. .
.
.
Randy
zpekic
Bruce Land
5-way seems easy :
2-way is 1 bit (easy).
3-way (6 permutations) requires 1+2 bits, with the 2-bit field using only 3 codes.
4-way (24) adds another 2-bit field, the new one is fully used.
5-way would require another 3-bit field that is not fully used. But we notice that 3×5=15, which fits in 4 bits. So the 3-bit field and the first 2-bit field can be merged.
So the 5-way full LRU permutations fit in 1+2+4=7 bits, which makes sense since 5!=120=2^7 - 8.
Interesting.
The remaining 8 codes can be used to indicate reset status for example.