All the dirty details and the preliminary design are described in this log:
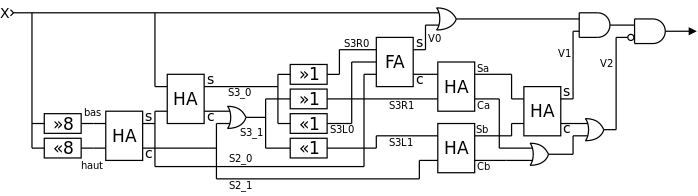
I have working equations and now I'll try to enhance the code, apply some graph analysis and optimise the register allocation to fit inside the 4-registers relay computer ( #YGREC-РЭС15-bis based on #AMBAP: A Modest Bitslice Architecture Proposal). Because YGREC has 16-bits wide registers, this code can update 16 cells per iteration, using the most out of this bare metal computer (litterally).
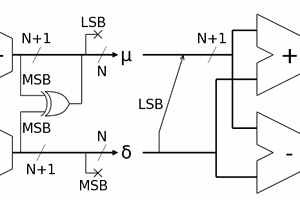
The computation uses 25 boolean operations and some more shifts (which can be factored in various ways). The YGREC datapath was being designed at the same time as this algorithm and, because it uses quite a lot of shift operations, it was decided that YGREC would include the shifter in front of the ALU, not in parallel like the YASEP.
However, bit shifting is only one aspect of the program: bit vectors must be correctly managed, dataflows must be optimised to reduce register spill.
For now I only care about running a world that is as wide as one register. In JavaScript, that's 32 bits, and 16 bits for AMBAP/YGREC. The length can be arbitrary though and I provide a C version with 64 bits.
Shrinking the code and saving an instruction here or there is not just a matter of beating a dead horse again. Conway's Game of Life is famous for having consumed incalculable amounts of CPU time and energy since its creation, decades ago. If you still need to be convinced that GoL is a computational blackhole, just look at people computing GoL with GoL, create Turing Machines, a computer, a clock, or other crazy GoL systems on YouTube.
But more down to earth, computing GoL on the #YGREC-РЭС15-bis is a challenge in itself, due to the slow clock (around 25 instructions per second), very limited and expensive parts and storage (very few registers and less than 1K bytes of DRAM) and all the instructions must be coded by hand on DIP switches!
Logs:
1. The parallel boolean computation
2. Handling data
3. So it works.
@Jean-François Poilpret designed #Conway's Game of Life on ATtiny84 for the The 1kB Challenge using the ideas of this algorithm and introduced some conceptual enhancements, which I have to examine in order to write an even better version. He explains thusly:
Hi Yann, calculating the full popcount was intentional, to be consistent at this level of computation. I did not change the rules of the game though, I just rephrased them to fit the whole count:
- any count other than 3 or 4 means a dead cell
- a count of 3 means that the cell must be live, whatever its previous state
- a count of 4 means that the cell must keep its previous state
So it seems my optimised version is still not optimal :-D
Here is the author's own definition:
 Yann Guidon / YGDES
Yann Guidon / YGDES



 Bruce Land
Bruce Land
Oh my, just thinking about this discussion makes me realize there are much more optimisations left :-D