The basic construction of the plotter consists of a thin wooden plate (3mm) which is glued onto a thicker wooden frame to increase the stability while being not too heavy.
All the mechanic stuff is from http://openbuildspartstore.com/, it's not to expensive and even if it's IMHO not best quality it does a good job as far as I can judge. Also this saves on brain which is needed for the programming part.
The electrics consist of a teensy and SilentStepStick TMC2209 drivers. I guess I'll need the raw power of the teensy because efficient programming is out of my league.
The initial alpha firmware can be found at github.
 sei
sei








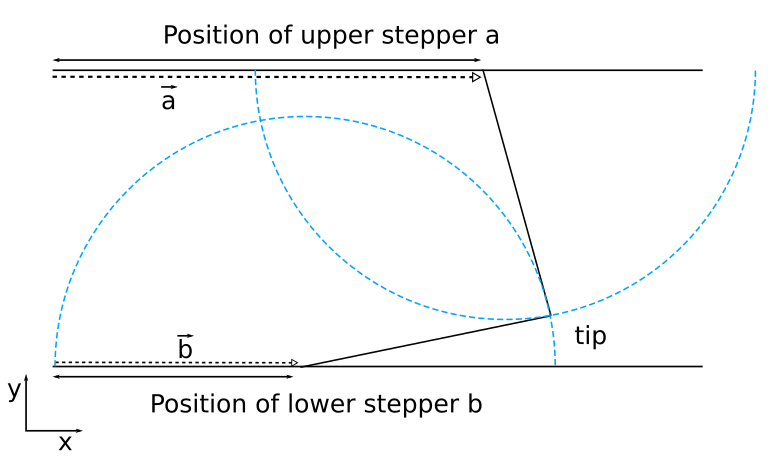
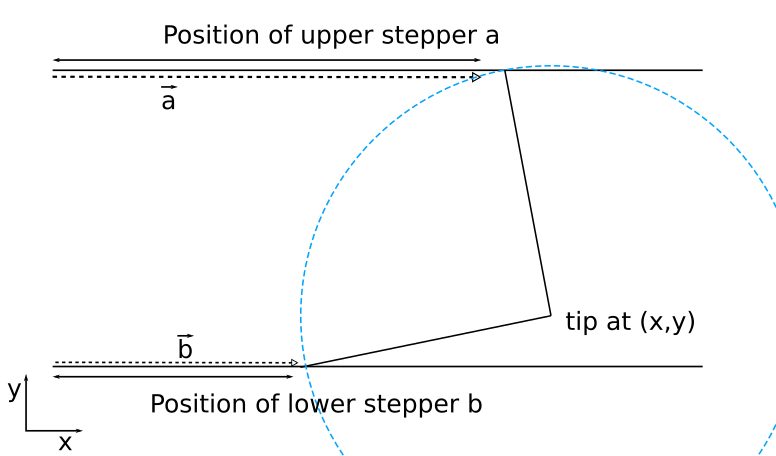



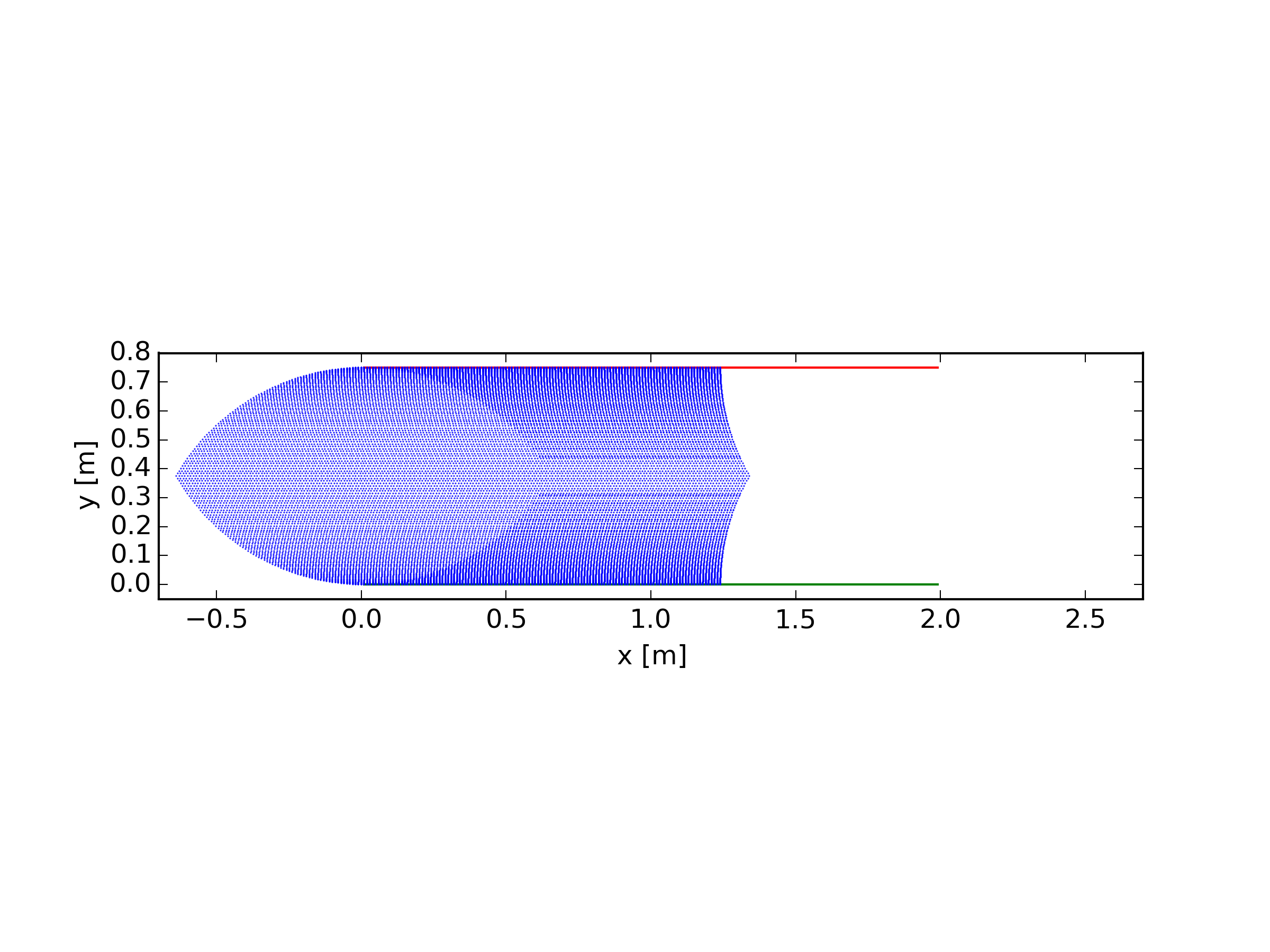
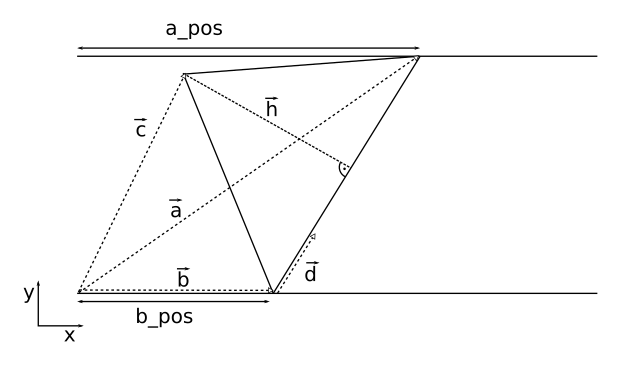



 Paul Crouch
Paul Crouch
 Thomas
Thomas
 johnowhitaker
johnowhitaker
 Jeroen Delcour
Jeroen Delcour
you should have a look at this website...
https://www.blackstripes.nl/de/products/drawbot/BOTMK2/