-
HackChat: The First 42 Posters
01/10/2018 at 16:47 • 2 comments![]()
... perhaps the next 42 should be a bit less dark ;)
-
System.nanoTime() for fun and profit
11/01/2017 at 16:53 • 0 commentsI was reading Colin O'Flynn's excellent "Forget Not the Humble Timing Attack" article in PoC | GTFO this morning, and I thought I should check how easy timing attacks would be in Java (I know, I know...).
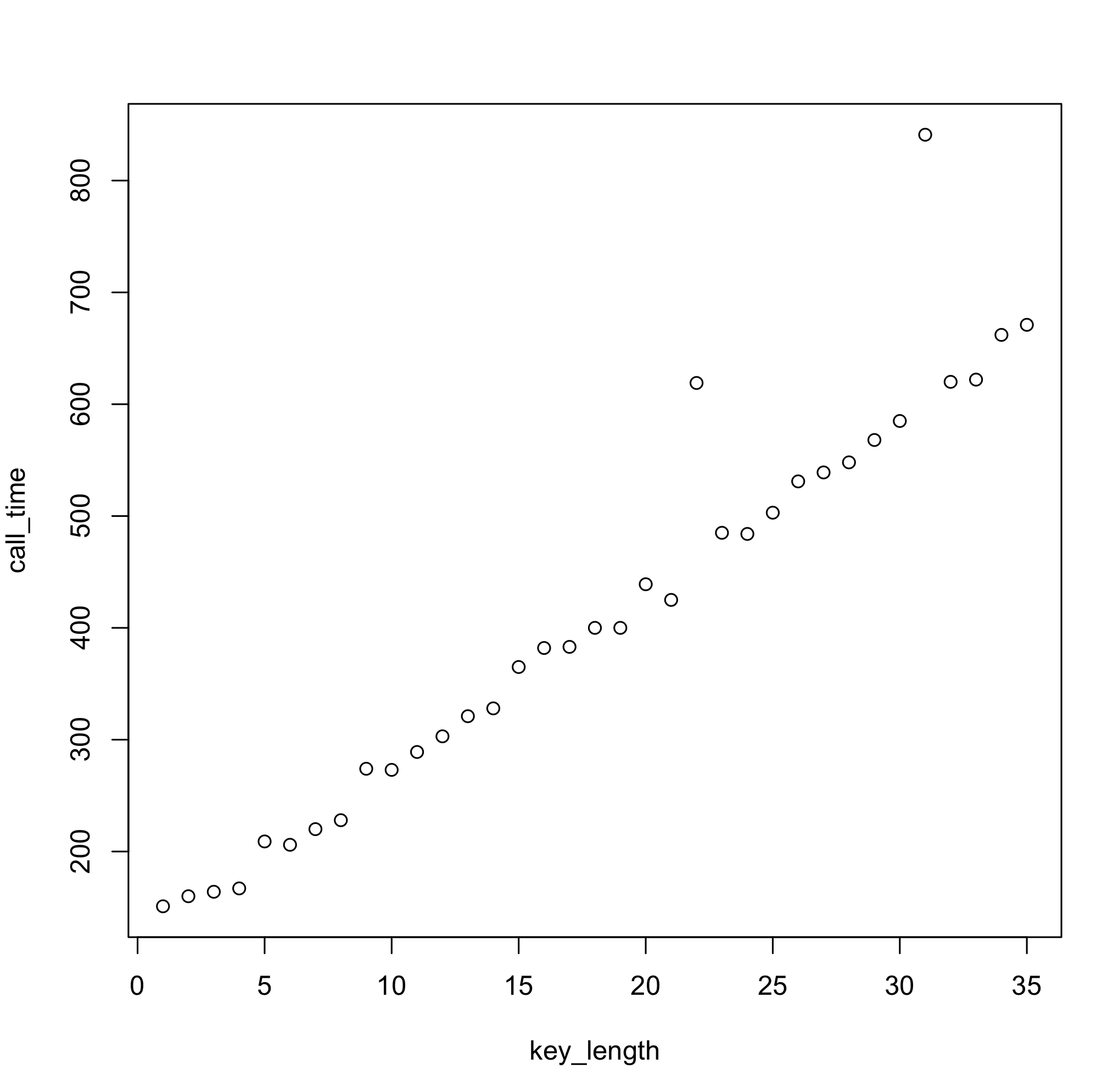
Anyway, turns out the System.nanoTime() is quite handy. Here's the sample demo that uses it to measure method invocation times for different key sizes:
import java.util.UUID; import java.util.Arrays; public class TimingPoC { private static char[] secret = UUID.randomUUID().toString().toCharArray(); /** leaky password check **/ public boolean checkSecret(char[] pwd) { for (int i=0; i<pwd.length; i++) { if (pwd[i] != secret[i]) { return false; } } return true; } public void start() { for (int i=1; i<secret.length; i++) { char[] candidate = Arrays.copyOfRange(secret, 0, i); long[] times = new long[5]; for (int it=0; it<times.length; it++) { long start = System.nanoTime(); checkSecret(candidate); times[it] = (System.nanoTime() - start); } Arrays.sort(times); System.out.println(i + "\t" + times[(int)Math.floor(times.length/2)]); } } }And here are the corresponding (nanosecond) response times:
![]()
One simple linear regression later...
Call: lm(formula = call_time ~ key_length) Residuals: Min 1Q Median 3Q Max -37.185 -21.977 -10.429 -1.134 214.983 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 111.9210 16.7010 6.701 1.24e-07 *** key_length 16.5838 0.8092 20.495 < 2e-16 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 48.35 on 33 degrees of freedom Multiple R-squared: 0.9272, Adjusted R-squared: 0.925 F-statistic: 420 on 1 and 33 DF, p-value: < 2.2e-16We can easily conclude that every extra character in the key length increases the method response time by 16.5 nanoseconds, which is the information that given naive password check information leaks. Now, all we need to do is keep increasing test key length until response times stop growing, and we'll have our target key size.
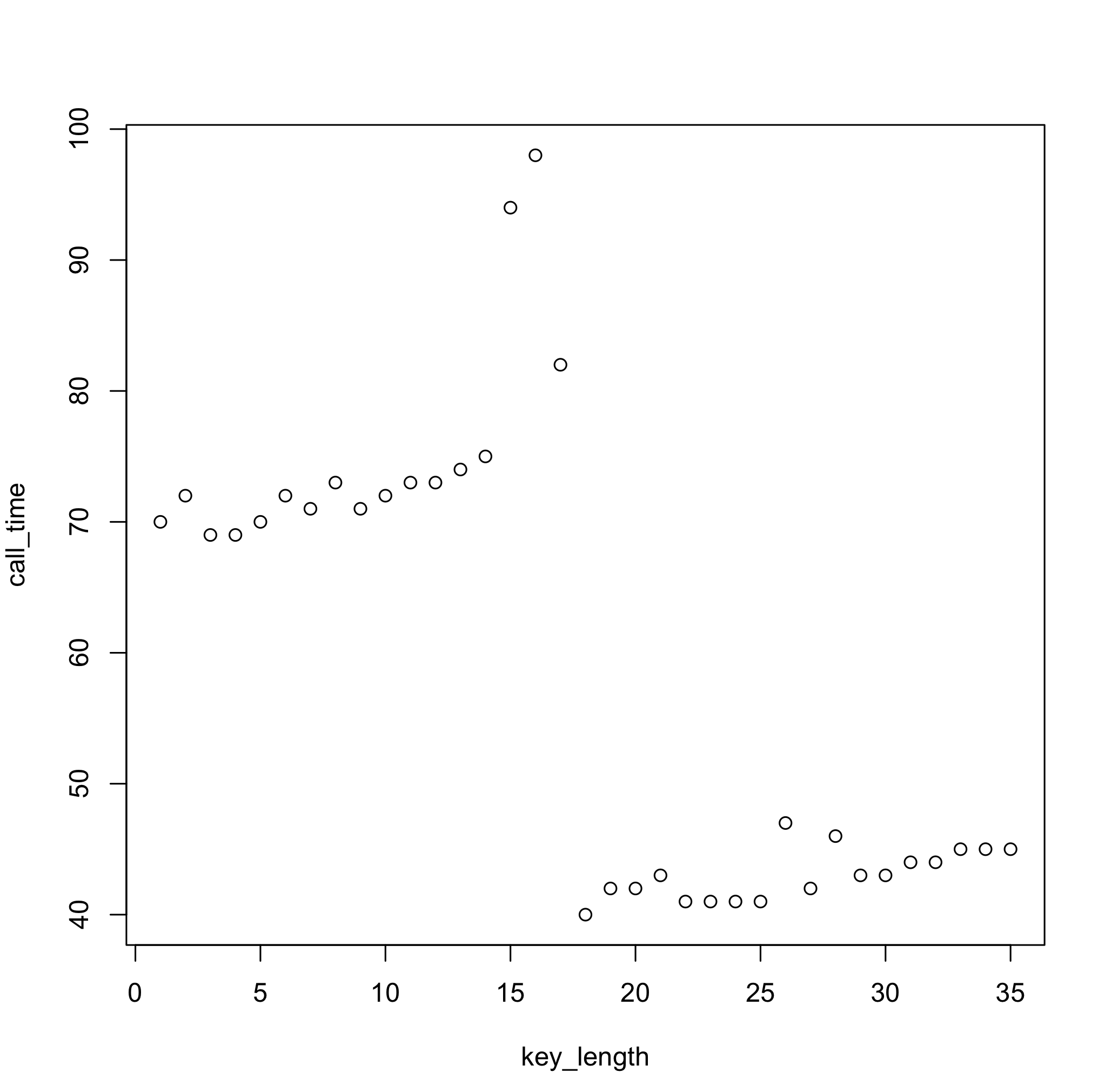
One thing to keep in mind with the approach above is that, on a modern OS, given times will not be deterministic. So repeated measurements are needed in order to get a "smoothed" value (in the code above value used is the median of 5 measurements). That said, though, in purely statistical terms, even more measurements would yield a more stable estimate, in this particular case, it's not necessarily true. Here's an example of a median based on 5000 samples:
![]()
Why do you think this is the case? :)
-
Random Bits & Pieces
12/26/2016 at 20:56 • 0 comments
Read more »
My Projects
Projects I Contribute To
My Events
My Pages
Things I've Built
uRSA
FPGA RSA Crypto Core on Xilinx Spartan-II
Projects I Like & Follow
Share this profile
ShareBits
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.
Thanks for following my Ultra-Low Power LiPo Charger via Energy Harvesting project!
Good afternoon Aleksander and thanks for following me. I do tend to construct things a bit different from most :-)
Thank you for following https://hackaday.io/project/11779-shared-silicon :)
Thanks for liking #Ankle Booster . Will you be at balccon in novisad?
Nah :\ Somehow I always miss it. Hopefully next year!
Hey Aleksandar, thanks for following #Cardware! Thanks to the seed funding I'll now be developing this further shortly. :-)
Thanks so much for supporting my work, it means a lot! :-) #DECAL is shaping up to be a generational development to Cardware, it was supposed to be 'a robot' ;-)
Hi Aleksandar, thanks for the follow. I noticed the cool Hackaday artwork in my feed, wondered who the artist was... :-)
Hi Aleksandar. Thanks for following #Joy232 too! I've just uploaded a video showing it in action.
Thank you for the like on my retro futuristic automobile control panel project. I am sorry for the long delayed answer.



 Aleksandar Bradic
Aleksandar Bradic Lutetium
Lutetium Benchoff
Benchoff Tindie
Tindie Supplyframe DesignLab
Supplyframe DesignLab
 Lucas LucidVR
Lucas LucidVR OxiKit
OxiKit ciprian
ciprian TuckerShannon
TuckerShannon pcadic
pcadic awkward intelligence
awkward intelligence Trevor Flowers
Trevor Flowers Merocle
Merocle roscale
roscale David Greenberg
David Greenberg CarL0
CarL0 ElectroBoy
ElectroBoy Alex
Alex dearuserhron
dearuserhron














Thanks for your interest in my TMD-2: Turing Machine Demonstrator Mark 2 project Aleksandar.